Теорема Жегалкина

Каждая функция из может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

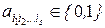, s = 0, 1, ..., n.

Определение.Функция f(x₁, ..., x_n), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а_{0 Å}а₁х_{1 Å}а₂х_{2 Å}... Åа_nх_n, называется линейной.

Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Определение: Говорят, что функция f(x₁, ..., x_n) сохраняет константу a Î {0, 1}, если f(a, …, a) = a.

Пример 4. Функция xy сохраняет 0, сохраняет 1. Функция x®y сохраняет 1 и не сохраняет 0.

Замыкание и замкнутые классы

Определение . Пусть MÍР₂. Замыканием М называется множество всех функций из P₂, которые можно выразить формулами над М. Замыкание М обозначается [M].

Определение .Множество функций М называется замкнутым классом, если [M]=M.

Пример 1.

1) P₂ – замкнутый класс.

2) Множество {1,x_1Åx₂} не является замкнутым классом. Его замыканием будет класс линейных функций: [{1, x_{1 Å}x₂}] = {f(x₁, ..., x_n) = c_{0 Å}c₁x_{1 Å} Åc_nx_n}. Действительно, по определению формулы над М, функция f(G₁, x₃), где f – есть сумма по модулю 2, G₁ – функция х_{1 Å}х₂, будет формулой над М: f(G₁, x₃) = (x_{1 Å}x₂) Åx₃.

Замечание.В терминах замыкания и замкнутого класса можно дать другое определение полноты, эквивалентное исходному:

М – полная система, если [M] = P₂.

Важнейшие замкнутые классы в Р₂

1) Т₀ - класс функций, сохраняющих константу 0.

Т₀ = { f(x₁, ..., x_n | f(0, ..., 0) = 0, n = 1, 2, ...}.

Примеры функций, входящих в Т₀:x₁&x₂, x_1Úx₂, xÎТ₀и примеры функций из Р₂, не входящих в Т₀: x₁|x₂, x₁x₂, ÏТ₀.

Число функций, зависящих от n переменных и принадлежащих Т₀, будет равно

2) T₁ – класс функций, сохраняющих константу 1.

T₁ = {f(x₁, ...) |f(1, 1, ...) = 1};

Функции x₁&x₂, x_1Úx₂, xÎT₁, х_1Åх₂, x₁x_2ÏT₁, следовательно Т₁ – собственное подмножество Р₂.

3) S – класс самодвойственных функций.

S = {f(x₁, ...)|f* = f };

Функции x, , x_1Åx_2Åx_3ÎS, x₁&x₂, x_1Úx₂, x_1Åx_2ÏS, следовательно, S – собственное подмножество Р₂. |S(n)| = .

4) L – класс линейных функций.

L = {f(x₁, ...)| f = c_0Åc₁x_1Å...Åc_nx_n};

Заметим, что тождественная функция принадлежит L и |L(n)| = 2ⁿ⁺¹.

5) М – класс монотонных функций.

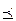
Определение. Набор = (a₁, ..., a_n) предшествует набору = (b₁, ..., b_n) и обозначается , если для 1£i£n a_i£b_i, например: = (0010), = (0110), тогда . Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования (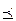) является отношением порядка на множестве наборов длины n, множество таких наборов будет частично упорядоченным множеством по отношению к операции.

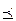
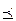Определение. Функция f(x₁, ..., x_n) называется монотонной, если для двух наборов и , таких что , выполняется f()f().

Функции 0, 1, x, x₁&x₂, x₁Úx_{2 Î}M, x₁¯x₂, x_{1 Å}x₂, x₁ ~ x_{2 Ï}M.

Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается.

Классы T₀, T₁, L, S, M пересекаются, но не совпадают, что видно из следующей таблицы, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.

	T0	T1	L	S	M
x	+	+	+	+	+
	-	-	+	+	-
	+	-	+	-	+
	-	+	+	-	+
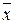
x1x2	+	+	-	-	+

A={x, 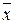, 0, 1, x₁x₂) не является полной системой функций так как всегда есть функции ÎР₂ не входящие в эти классы.