Основные этапы эконометрического моделирования и классификация моделей.
Для изучения различных экономических явлений экономисты используют их прощенные формальные описания, называемые экономическими моделями.
Модель – это условный образ объекта, построенный для упрощения его исследования. Математическая модель экономического объекта – это его отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности и даже в исследовании политических процессов.
В настоящее время эконометрика располагает огромным разнообразием типов моделей – от больших макроэкономических моделей, включающих несколько сот, а иногда и тысяч уравнений, до малых коинтеграционных моделей, предназначенных для решения специфических проблем.
К основным задачам эконометрики можно отнести следующие:
· Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа. Данную проблему принято называть проблемой спецификации. Зачастую она может быть решена несколькими способами.
· Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным. Это так называемый этап параметризации.
· Проверка качества найденных параметров модели и самой модели в целом. Иногда этап анализа называют этапом верификации.
· Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Можно выделить три основных класса моделей, которые применяются для анализа и / или прогноза.
1. Модели временных рядов.К этому классу относятся модели:
тренда: 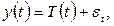
где T(t) – временной тренд заданного параметрического вида, 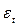 - случайная компонента;
- случайная компонента;
сезонности: 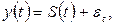
где S(t) – периодическая (сезонная) компонента, 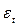 - случайная (стохастическая) компонента;
- случайная (стохастическая) компонента;
тренда и сезонности:  (аддитивная) или
(аддитивная) или
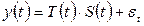 (мультипликативная),
(мультипликативная),
где T(t) – временной тренд заданного параметрического вида, S(t) – периодическая (сезонная) компонента, 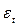 - случайная компонента.
- случайная компонента.
К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего и др. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования объема продаж авиабилетов, спроса на мороженое, краткосрочного прогноза процентных ставок и т.п.
2. Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная у представляется в виде функции  , где
, где 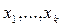 - независимые (объясняющие) переменные, а
- независимые (объясняющие) переменные, а 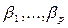 - параметры. В зависимости от вида функции
- параметры. В зависимости от вида функции 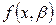 модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п.
модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п.
Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов.
3. Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, имеется набор объясняемых переменных, связанных через уравнения системы. Примером может служить модель спроса и предложения. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для моделей страновой экономики и др.
При моделировании экономических процессов мы встречаемся с двумя типами данных:
· пространственные данные;
· временные ряды.
Примером пространственных данных является, например, набор сведений (объем производства, количество работников, доход и др.) по разным фирмам в один и тот же момент времени (пространственный срез). Другим примером могут являться данные по курсам покупки/продажи наличной валюты в какой-то день по обменным пунктам города.
Примерами временных данных могут быть ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы или, например, ежедневный курс доллара США на ММВБ, цены фьючерсных контрактов на поставку доллара США (ММБ) и котировки ГКО (ММВБ) за два последних года.
Отличительной чертой временных данных является то, что они естественным образом упорядочены по времени, кроме того наблюдения в близкие моменты времени часто бывают зависимыми.
Процесс эконометрического моделирования происходит в течение нескольких этапов. В основе первого этапа статистического изучения связей лежит качественный анализ явления, связанный с анализом его природы методами экономической теории, социологии, конкретной экономики. Второй этап – построение модели связи. Он базируется на методах статистики: группировки, средних величин, таблиц и т.д. Третий этап – интерпретация результатов. Он вновь связан с качественными особенностями изучаемого явления.
Существует множество методов изучения связей, выбор конкретного из которых зависит от цели исследования и от поставленной задачи. Связи между признаками и явлениями классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса:
1. Факторные (факторы) – это признаки, обусловливающие изменение других, связанных с ними признаков.
2. Результативные – это признаки, изменяющиеся под действием факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению (выделяют прямую и обратную связь), по аналитическому выражению (выделяют прямолинейные – или просто линейные – и нелинейные - или криволинейные).
Для выявления наличия связи, ее характера и направления используются следующие методы: метод приведения параллельных данных (основан на сопоставлении двух или нескольких рядов статистических величин, что позволяет установить наличие связи и получить представление о ее характере), аналитических группировок, графический, корреляции и регрессии.
Глава 2
Парная регрессия и корреляция в эконометрических исследованиях.