Параграф 2.4.3:Описание поведения линейных систем в частной области

 

В частотной области сигналы представляются своими спектрами. Для того чтобы найти правило, связывающее спектры входного и выходного сигналов системы определим преобразование Фурье от обеих частей интеграла Дюамеля. Учитывая свойство 7 преобразования Фурье (теорема о свертке) имеем: , где и — преобразования Фурье сигналов U_вых(t) и U_вх(t), а 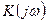— преобразование Фурье или комплексный спектр импульсной характеристики системы, т.е. .

Величина называется комплексной частотной характеристикой системы (КЧХ). Иногда ее называют так же частотным коэффициентом передачи, частотной передаточной функцией, амплитудно-фазовой характеристикой. Она является комплексной функцией частоты и может быть представлена в виде:

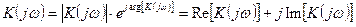
— АЧХ системы.

— ФЧХ системы.

В технике связи значение сигналов обычно характеризуются их уровнями, выраженных в логарифмических единицах (Дб или Нп), а разность между уровнями сигнала на выходе и входе канала называют остаточным затуханием. При этом под АЧХ канала понимают зависимость остаточного затухания от частоты. АЧХ показывает, как АЧХ измеряет амплитуду сигнала.

Из-за сложности измерения ФЧХ на практике обычно оперируют групповым временем прохождения (ГВП) представляющим собой производную ФЧХ по частоте, т.е.:

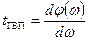
Существуют системы, у которых АЧХ и ФЧХ однозначно связаны между собой, они называются минимально фазовыми, также существуют системы, у которых АЧХ и ФЧХ не связаны, они называются не минимально фазовыми.

Поскольку КЧХ К(jω) есть комплексный спектр действительной функции h(t) модуль этой функции, т.е. АЧХ Является четной функцией частоты, а аргумент, т.е. ФЧХ φ(ω) является нечетной функцией.

Графики АЧХ и ФЧХ могут выглядеть, например, так:

 

По виду АЧХ можно судить о физической реализуемости системы.

Необходимым условием физической реализуемости системы является выполнение критерия (условия) Пэйли-Виннера, имеющего вид:

Если интеграл сходится то система физически реализуема.

Из этого условия следует, что АЧХ К(ω) может быть равна нулю на нескольких дискретных частотах (при этом , но Δω=0), но не может оставаться равной нулю в конечной полосе частот (при этом, - интеграл расходится). Кроме того, это условие ограничивает крутизну спада или подъема АЧХ физически реализуемой системы.

Предположим, что . Т.к. растет медленнее, чем знаменатель и критерий Пэйли-Винера выполняется, при этом система называется каузальной. Если же будет меняться по закону , то скорость роста числителя будет равна или выше скорости роста знаменателя. Интеграл будет расходящимся. Т.о. максимально возможная скорость изменения АЧХ физически реализуемой системы определяется экспоненциальной функцией. Приведенные рассуждения позволяют сделать вывод, что идеальные ФНЧ, ФВЧ, ПФ с характеристикой типа

являются физически нереализуемыми. Однако практически можно получить характеристики сколь угодно близкие к характеристикам идеальных фильтров за счет усложнения фильтров.

Предположим, что на вход системы поступает Uвх(t) = ,

Тогда в соответствии с интегралом Дюамеля

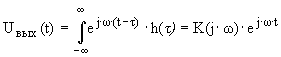
Подставляя эти значения U_вх(t) и U_вых(t) в дифференциальное уравнение общего вида, после сокращения на общий множительнаходим КЧХ в виде:

Полученное уравнение определяет связь КЧХ с коэффициентами дифференциального уравнения системы.

Существуют критерии, которые позволяют по виду КЧХ определить устойчивость системы и определить ее запас устойчивости, т.е. область возможных изменений параметров системы, при которых она остается устойчивой.

Параграф 2.4.4: Передаточная функция линейной системы

Если функции, описывающие входные выходные сигналы системы представлены с помощью соответствий или преобразований Лапласа в виде U_вых(р) и U_вх(р), то правила, связывающие U_вых(р) и U_вх(р) можно получить вычислив преобразование Лапласа от обеих частей интеграла Дюамеля; учитывая, что при переходе к изображением свертка заменяется произведением, получим:

Здесь К(р) = L[h(t)] – передаточная функция системы, представляющая собой преобразование Лапласа от ее импульсной характеристики.

Р = σ + jω комплексная переменная.

Пусть линейная система задана своим дифференциальным уравнением (2.13). Полагая начальные условия нулевыми вычислим преобразование Лапласа от обеих частей (2.13). В результате получим:

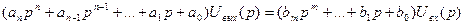
откуда

(*)

Полученные соотношения связывают передаточную функцию системы с коэффициентами ее дифференциального уравнения, сопоставляя его с аналитическим выражением для К(jω), нетрудно убедиться, что КЧХ К(jω) представляет собой передаточную функцию К(р), вычисленную на линейной оси комплексной точности, определяемой уравнением Р = jω.

Практически это означает, что для того, чтобы от выражения для К(р) перейти к выражению для К(jω) необходимо всего лишь заменить оператор Р на jω.

Выражение (*) показывает, что передаточная функция K(P) представляет собой дробно-рациональную функцию комплексной переменой Р. Условием физической системы с передаточной функцией К(Р) является выполнение неравенства . Если приравнять знаменатель (*) к нулю, то получим уравнение 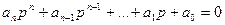. Корни этого уравнения 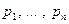называются полюсами функций К(Р). Приравнивая к 0 числитель этого выражения получаем уравнение . Корни этого уравнения называются нулями передаточной функции.

Полюсы и нули называются особыми точками передаточной функции. Зная полюсы и нули передаточной функции можно восстановить ее с точностью до константы К0, записав, . Расположение особых точек в Р плоскости характеризует свойства системы. Полюсы передаточной функции являются корнями выражения (*), которое совпадает с характеристическим уравнением системы (см. пункт 2.4.2.2). Поэтому для устойчивости системы необходимо и достаточно, чтобы полюсы располагались строго в левой полуплоскости переменной Р. Нули передаточной функции в общем случае могут располагаться как в левой, так и в правой полуплоскости. Однако их расположение также оказывает существенное влияние на свойство системы. В том случае, если передаточная функция не имеет нулей в правой полуплоскости, то соответствующая ей линейная устойчивая система называется минимально-фазовой. Если же нули в правой полуплоскости имеются, то система является неминимально-фазовой.