Работа элементарных лопастей ветроколеса. Первое уравнение связи

Теория реального ветряка

II. Resumez le texte lu.

 

 

 

 

 

Выделимиз лопастей ветроколеса двумя концентрическими окружно-

 

стямис радиусами r и

 

r +dr

 

кольцевуюповерхность

 

dF =2prdr .Это коль-

 

цо на крыльях вырежет отрезки длиною dr , которые называются элементар-

 

нымилопастями (рис. 8.1.1). Через все точки обеих окружностей проведем

 

линиитока,образующиедвеповерхностиABC ,

 

A¢B¢C ¢ бутылеобразнойфор-

 

мы (рис. 8.1.2). Жидкость, заключённую между этими поверхностями,

 

назовёмэлементарной кольцевой струёй.

 

 

Рис. 8.1.1. Выделение элементарных лопастей на ветроколесе.

 

 

Сделаем предположение, обычно принимаемое в аналогичных теориях, что разность давлений по обе стороны ветрового колеса, действующая на площадь кольца, получающегося от пересечения ометаемой плоскостью эле- ментарной струи, воспринимается элементарными лопастями.

На основании этого составляем первое уравнение связи:

2prdr( p1 - p2 ) = i(dY cos b + dX sin b ), (8.1.1)

 

где Y – подъемная сила крыла, направленная перпендикулярно потоку;

 

X – сила сопротивления крыла (лобовое сопротивление крыла), направ-

 

 

ленная по потоку;

 

b – угол между плоскостью вращения ветроколеса и направлением воз-

 

душного потока, набегающего на крыло;

 

i– число лопастей ветроколеса.

 

Рис. 8.1.2. Элементарная кольцевая струя.

 

 

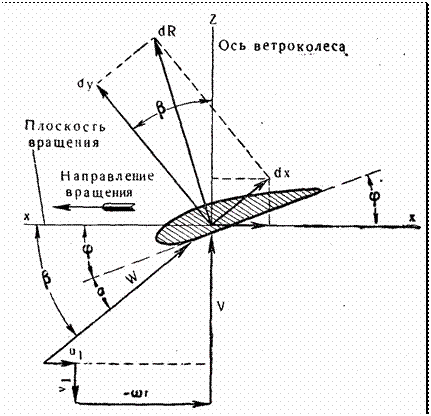
Для определения направления сил, действующих на элементарную ло-

 

пасть, изобразим ее сечение на рисунке 8.1.3, где ось Z направлена по оси

 

ветроколеса и ось

 

x -x

 

в плоскости его вращения; V – направление скоро-

 

сти ветра; W – направление скорости относительного потока, набегающего

 

на элемент лопасти.

Разложим силу dR , действующую на элементарную лопасть, на две си- лы: dX , действующую по потоку, и dY , направленную перпендикулярно по- току. Сила dX вызывает сопротивление элемента крыла; dY вызывает ок- ружное усилие элемента крыла и называется подъёмной силой.

 

Вследствие вращения ветроколеса в плоскости

 

x -x

 

воздушный поток

 

набегает на ветроколесо не со скоростью ветра V , а с относительной скоро-

 

стью W , которая слагается геометрически из скорости ветра V и окружной скорости wr , где w угловая скорость и r – расстояние элемента лопасти от

оси вращения ветроколеса.

Скорость потока, набегающего на элемент лопасти, в относительном движении будет равна:

 

 

V

W = 2

+(-wr-u1

)2 , (8.1.2)

 

где V1 =V

-v1 – скорость ветра в плоскости ветряка.

 

 

Рис. 8.1.3. План скоростей воздушного потока при набегании его на элемент

лопасти.

 

 

Скорость u1 получается как реакция от крутящего момента, развивае- мого лопастями. Эта скорость имеет направление, обратное моменту; её ве- личина берётся как средняя для всей зоны, в которой работают лопасти. В действительности эта скорость перед ветроколесом равна нулю и непосред- ственно за ветряком равна u 2 . Так как закон изменения этой скорости неиз- вестен, то, как первое приближение, её принимают равной:

u =u 2 . (8.1.3)

1 2

 

Силы dY и dX можно выразить как:

 

 

dY = C

 

bdrrW2, (8.1.4)

y 2

 

 

 

 

dX = C

bdrrW2 , (8.1.5)

x 2

 

где b – ширина элемента лопасти по хорде.

 

Кроме того, на основании уравнения для лобового давления на ветряк

 

(потеории идеального ветряка Г.Х. Сабинина) можем написать:

 

P

p1 -p2 =

F1

 

= rVv2

 

. (8.1.6)

 

Подставляя вместо dY и dX и

 

получим:

p1 -p2

их значения в уравнение (8.1.1),

 

 

2prdrrVv2

=i⎛bdrC

⎜

y

⎝

rW2 cos b+bdrC

2 x

rW2 sin b⎞; (8.1.7)

⎟

2 ⎠

 

после сокращения получим:

 

W 2 ⎛ C ⎞

2prVv

=ibdrC

cos b⎜1 + x tgb⎟; (8.1.7а)

 

 

или

y ⎜ ⎟

C

⎝ y ⎠

 

⎛ C ⎞

4prVv

=ibdrC

W2 cosb⎜1+ x tgb⎟. (8.1.7б)

C

2 y ⎜ ⎟

⎝ y ⎠

 

На основании рис. 8.1.3 можно ввести обозначение

 

wr +u1

ctgb =

 

V -v1

=zu , (8.1.8)

 

которое называют числом относительных модулей.

 

Из уравнения (8.1.8) имеем:

 

 

или

- wr - u1 = - zu (V

- v1 ), (8.1.8а)

 

(-wr -u1 )

 

u

= z 2 (V

 

-v1

 

u

)2 , (8.1.8б)

 

u

и, зная, что V1 =V

-v1 , уравнение (8.1.2) можем переписать так:

 

W = (V

-v1)

+ z 2(V

-v1)

= (V

-v1)

1 + z 2. (8.1.9)

 

Заменим:

 

 

sin b=V

-v1 =

V -v1

= 1 , (8.1.10)

u

W (V

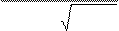
-v1 )

1 + z 2

1 + z 2

 

cosb=wr +u1 =

wr +u1

= zu

 

u

, (8.1.11)

u

u

W (V

-v1 )

1 + z 2

1 + z 2

 

tgb=1

zu

 

, (8.1.12)

 

C x =m

C y

 

– обратное качество крыла(8.1.13)

 

и подставим их в уравнение (8.1.7б)

 

z

 

 

⎛ m⎞

4prVv

 

=ibC

(V -v

)2(1+z 2) u ⎜1+

⎟. (8.1.7в)

2 y 1

u

u

1 + z 2 ⎝

 

v

zu ⎠

Вводя в это уравнение

 

 

v =2v1 ,получим:

1+v1

V

e = 1изаменив

V

v2 его значением из равенства

 

 

ibC y

 

= 8pr

e

(1 + e)(1 + e)2

 

 

(zu

+ m )

 

 

u

1 + z 2

 

. (8.1.14)

 

Это уравнение называется уравнением связи; оно связывает ширину

 

лопасти и коэффициент подъемной силы с деформацией потока, характери-

 

зуемой величиной e .

Взяв сумму проекций сил элемента лопасти на касательную к окружно- сти, по которой он движется, получим окружное усилие, развиваемое эле- ментарными лопастями:

dQ =ibdr rW 2 (C

2 y

 

sin b - C x

 

cos b ).

 

 

чим:

 

Подставляя сюда значение W , sin b

 

и cos b

 

и вводя C x

 

= mC y , полу-

 

 

 

dQ =ibdr r(V

 

u

y

- v1

)2 (1 + z 2 )C

1-mzu

u

1 + z 2

 

. (8.1.15)

 

Подставляясюда значение ibC y

 

щения,получим:

из уравнения (8.1.14) и сделав сокра-

 

 

dQ =4prdrr

 

e V 2 1 -mzu

 

 

. (8.1.16)

1 + e

zu +m

 

Момент относительно оси ветряка равен:

 

 

dM =dQr =4pr 2 drr

 

e V 2 1 -mzu

 

 

. (8.1.17)

1 + e

zu +m

 

Секундная работа элементарных лопастей:

 

 

dT =dMw=4prdrr

 

e V 3

 

1 - mzu

 

 

z . (8.1.18)

1 + e

zu +m

 

Секундная энергия далеко перед ветряком, заключенная в потоке, пло-

 

щадь сечения которого определяется площадью кольца, сметаемого элемен-

 

тарными лопастями, равна:

 

V 3

dT0

= 2prdrr

. (8.1.18а)

 

Поделив секундную работу элементарных лопастей на эту энергию,

 

получим элементарный коэффициентиспользования энергии ветра:

 

x=dT =

 

4e 1 -mzu

 

 

z . (8.1.19)

dT0

1 + e

zu +m

Умножив и разделив выражение (8.1.19) на (1 -e)получим:

 

x=4e 1 -e 1 -mzu

z . (8.1.19а)

1 + e

zu +m1 -e

 

 

Так как выражение

4e 1 -e

1 +e

 

представляет идеальный коэффициент

 

использованияэнергии ветра, то можем написать:

 

 

i

x=x

 

1 - mzu

 

i

z =xh, (8.1.20)

zu +m1 -e

 

 

где

 

 

h=1 -mzu z

 

(8.1.21)

zu +m1 -e

 

называют относительным коэффициентом полезного действияэлемен-

 

тарного ветряка.

 

При большом числе модулей можно приблизительно считать:

 

z @z

1 - e u

 

и тогда:

 

h=1 -mzu z

 

 

(8.1.21а)

zu +m1 -e

 

Напомним, что числом модулей, или быстроходностьюветродвигате-

 

ля, называют отношение окружной скорости конца лопасти к скорости ветра:

 

Z =wR .

V

 

Число модулей элементов лопастей на радиусе r равно:

 

z =wr . (8.1.22)

V

 

Число модулей для любого радиуса r ветряка с известной быстроход-

 

ностью Z может быть выражено так:

 

 

z = Z

r , (8.1.23)

R

 

где R – радиус ветроколеса.