Работа поверхности при действии на нее силы ветра
Классификация ветродвигателей по принципу работы
Существующие системы ветродвигателей по схеме устройства ветро-
колеса и его положению в потоке ветра разделяются на три класса.
Первый классвключает ветродвигатели, у которых ветровое колесо располагается в вертикальной плоскости; при этом плоскость вращения пер- пендикулярна направлению ветра, и, следовательно, ось ветроколеса парал- лельна потоку. Такие ветродвигатели называются крыльчатыми.
Быстроходностью называется отношение окружной скорости конца ло-
пасти к скорости ветра:
Z =wR . (6.2.1)
V
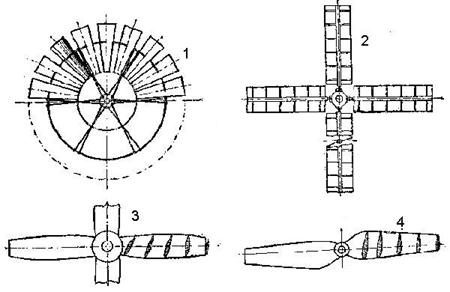
Крыльчатые ветродвигатели, согласно ГОСТ 2656-44, в зависимости от типа ветроколеса и быстроходности, разделяются на три группы (рис. 6.2.1).
- ветродвигатели многолопастные, тихоходные, с быстроходностью
Z n £2 .
- ветродвигатели малолопастные, тихоходные, в том числе ветряные
мельницы, с быстроходностью
Z n >2 .
- ветродвигатели малолопастные, быстроходные,
Z n ³3 .
Ко второму классуотносятся системы ветродвигателей с вертикаль-
ной осью вращения ветрового колеса. По конструктивной схеме они разби-
ваются на группы:
- карусельные, у которых нерабочие лопасти либо прикрываются шир-
мой, либо располагаются ребром против ветра;
- роторные ветродвигатели системы Савониуса.
К третьему классуотносятся ветродвигатели, работающие по принци-
пу водяного мельничного колеса и называемые барабанными. У этих ветродвигателей ось вращения горизонтальна и перпендикулярна
направлению ветра.
|
ных; 2-4 - малолопастных
Основные недостатки карусельных и барабанных ветродвигателей вы-
текают из самого принципа расположения рабочих поверхностей ветроколеса
в потоке ветра, а именно:
1. Так как рабочие лопасти колеса перемещаются в направлении воз- душного потока, ветровая нагрузка действует не одновременно на все лопа- сти, а поочерёдно. В результате каждая лопасть испытывает прерывную на- грузку, коэффициент использования энергии ветра получается весьма низким
и не превышает 10%, что установлено экспериментальными исследованиями.
2. Движение поверхностей ветроколеса в направлении ветра не позво- ляет развить большие обороты, так как поверхности не могут двигаться бы- стрее ветра.
3. Размеры используемой части воздушного потока (ометаемая поверх- ность) малы по сравнению с размерами самого колеса, что значительно уве- личивает его вес, отнесённый к единице установленной мощности ветро- двигателя.
У роторных ветродвигателей системы Савониуса наибольший коэффи-
циент использования энергии ветра 18%.
Крыльчатые ветродвигатели свободны от перечисленных выше недос-
татков карусельных и барабанных ветродвигателей. Хорошие аэродинамиче-
ские качества крыльчатых ветродвигателей, конструктивная возможность из- готовлять их на большую мощность, относительно лёгкий вес на единицу мощности – основные преимущества ветродвигателей этого класса.
Коммерческое применение крыльчатых ветродвигателей началось с
1980 года. За последние 14 лет мощность ветродвигателей увеличилась в 100
раз: от 20-60 кВт при диаметре ротора около 20 м в начале 1980 годов до
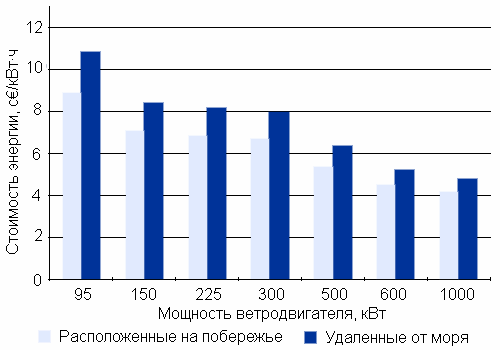
5000 кВт при диаметре ротора свыше 100 м к 2003 году (рис. 6.2.2). Некото- рые прототипы ветродвигателей имеют еще большие мощность и диаметр ротора. За тот же период стоимость генерируемой ветряками энергии снизи- лась на 80 % [4]. Зависимость стоимости электроэнергии от мощности ветродвигателей при их расположении на побережье и вдали от моря
представлена на рис. 6.2.3 (в ценах 2001 г.).
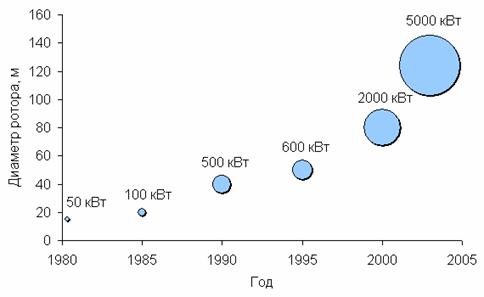
Рис. 6.2.2. Рост мощности и диаметра ротора коммерческих ветродвигателей
|
телей при их расположении на побережье и вдали от моря
Скоростью ветраназывают расстояние в метрах, проходимое массой воздуха в течение одной секунды. Скорость ветра постоянно меняется по ве- личине и направлению. Причиной этих изменений является неравномерное нагревание земной поверхности и неровности рельефа местности.
Скорость ветра является важнейшей характеристикой технических свойств ветра. Поток ветра с поперечным сечением F обладает кинетиче- ской энергией, определяемой выражением:
mV 2
. (6.3.1)
Масса воздуха, протекающая через поперечное сечение F со скоро-
стью V , равна:
m = rFV . (6.3.2)
Подставив (6.3.2) в выражение кинетической энергии (6.3.1), получим:
mV2
rFV 3
= , (6.3.3)
откуда следует, что энергия ветра изменяется пропорционально кубу его ско-
рости.
Посмотрим, сколько процентов энергии ветра может превратить в по- лезную работу поверхность, поставленная перпендикулярно к направлению ветра и перемещающаяся в этом же направлении, что имеет место, например,
у ветродвигателей карусельного типа.
| Мощность T определяется произведением силы | P | на скорость V : |
| T = PV . | (6.3.4) |
Одну и ту же работу можно получить либо за счёт большой силы, при
малой скорости перемещения рабочей поверхности, либо, наоборот, за счёт малой силы, а следовательно, и малой поверхности, но при соответственно увеличенной скорости её перемещения.
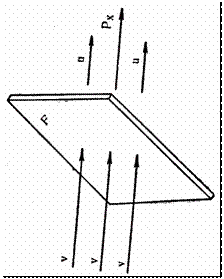
Допустим, мы имеем поверхность F, поставленную перпендикулярно к направлению ветра. Воздушный поток вследствие торможения его поверхно- стью получит подпор и будет обтекать её и производить давление силой Px . Вследствие действия этой силы поверхность будет перемещаться в направ- лении потока с некоторой скоростью U (рис. 6.3.3); работа при этом будет равна произведению силы на скорость U , с которой перемещается поверх- ность F, т. е.:
T=PxU, (6.3.5)
где
Px – сила сопротивления, которая равна :
Px= C xF
r(V
- U )2, (6.3.6)
где C x
– аэродинамический коэффициент лобового сопротивления;
F – поверхность миделевого сечения теля, т.е. проекции площади тела на
плоскость, перпендикулярную направлению воздушного потока.
В этом случае ветер набегает на поверхность с относительной скоро-
стью, равной :
W = V
- U . (6.3.7)
чим:
Подставив значение
Px из уравнения (6.3.6) в уравнение (6.3.5), полу-
T = C xF
r(V
- U )2U , (6.3.8)
Рис. 6.3.3. Действие силы ветра на поверхность.
Определим отношение работы, развиваемой движущейся поверхно- стью и выраженной уравнением (6.3.8), к энергии ветрового потока, имею- щего поперечное сечение, равное этой поверхности, а именно:
|
-U )2 U
x= 2 =C (V
rV 3 x
-U )2 U
V 3
. (6.3.9)
F
После преобразований получим:
x = C
⎛
x ⎜1 -
⎝
U ⎞2 U
⎟
V ⎠ V
. (6.3.10)
Величину x называют коэффициентом использования энергии ветра.
Из уравнения (6.3.10) мы видим, что x зависит от скорости перемеще- ния поверхности в направлении ветра. При некотором значении скорости U коэффициент x получает максимальное значение. В самом деле, если ско- рость перемещения поверхности равна нулю U = 0 , то работа ветра также
равна нулю. Если U = V ,т.е. поверхность перемещается со скоростью ветра,
работа также будет равна нулю, так как нет силы сопротивления, за счёт ко-
торой совершается работа. Отсюда следует, что значение скорости U заклю-
чено в пределах между U =0
и U =V .
Установлено, чтобы получить максимальное x , поверхность должна перемещаться со скоростью:
U =1 V . (6.3.11)
Максимальный коэффициент использования энергии ветра при работе поверхности силой сопротивления не может быть больше x = 0,192 .