Решение дифференциальных уравнений в частных производных.

Литература

. . .

B2 ® S2 Si – оператор или их последовательность

Если S –программа, то Pи Qзадают логическую спецификацию программы.

P { S }Q– тройка Хоара:

S -программа или фрагмент программы;

P- предусловие – предикат, характеризующий множество начальных состояний;

Q -постусловие – предикат, характеризующий множество конечных состояний.

Примеры:

1. Вычислить приближенное значение R - корня квадратного из N

(R округляется до целого): { N >= 0 } S { R² =< N < (R + 1)² }

2. Упорядочить по возрастанию числовой массив из n элементов:

{ N > 0 } S { "i : 0 £ i £ n-2: b[i] £ b[i + 1] }

(Задание 2)

Цель верификации – доказать, что если до выполнения программы истинно P, то программа завершается в состоянии истинности Q.Идея Хоара: описать семантику каждого оператора языка программирования формально и использовать эти утверждения для доказательства программы. Семантика описывается т.н. наислабейшим предусловием wp (weakest predicate). Это – функция программы (фрагмента программы, оператора) S и постусловия R. Функция wp (S, R) описывает множество всех состояний, для которых выполнение S обязательно закончится через конечное время в состоянии, удовлетворяющем R.

Например, wp ( ‘i:= i + 1; i £ 1 ) = ( i £ 0 ) . Заметим, что ( i < - 5 ) – тоже предикат, истинный для S, R, но более сильный, чем ( i £ 0 ).

Q { S } R – другая форма записи предиката Q Þ wp ( S, R ), где Þ - знак импликации. wp как функция обладает определенными свойствами, например:

· wp (S, Q) & wp (S, R) = wp (S, Q & R) – дистрибутивность конъюнкции

· Если Q Þ R, то wp (S, Q) Þ wp (S, R) – закон монотонности

Эти и другие свойства используются при формальной верификации.

Аксиоматическое задание семантики операторов

1. Последовательность операторов S1; S2

wp ( 'S1; S2', R ) = wp (S1, wp ( S2, R )), поскольку wp ( S2, R ) - это постусловие для S1.

2. Оператор присваивания: wp ( 'x:= e', R ) = R _x _¬_e

(т.е., в предикате R все вхождения x заменены на e).

Например, wp ( ‘x = 2 * y + 3 ‘, x = 13 ) = ( 2*y + 3 = 13) = (y = 5)

3. Оператор выбора IF (аналог оператора case):

ifB₁ ® S1 где: B_i – предохранители - предикаты

B_n ® SN

· На порядок проверки предохранителей не накладывается ограничений: если несколько из них истинны, то недетерминизм

· Если некоторый B_i не определен или ни один из них не истина, то программа прекращается (аварийный останов - авост)

Основная теорема для IF

Пусть предикат Q таков, что:

1) Q Þ B₁Ú B₂Ú ... Ú B_n

2) Q & B_iÞ wp ( Si, R ) ( 1 £ i £ n )

Тогда и только тогда Q Þ wp ( IF, R)

Используя три описанных оператора, можно синтезировать простейшую программу одновременно с доказательством ее правильности. Пример: для фиксированных x, y найти максимальный их них. Формальная спф задачи:

{ T } S { R: z = max (x, y) };

логическое определение функции max: R: (z = x Ú z = y) & z ³ x & z ³ y

Какую команду выполнить, чтобы получилось R ? Попробуем z := x. Когда она должна выполниться ?

Wp( ‘z:=x’, R ) =

= ( x = x Ú x = y) & x ³ x & x ³ y =

= ( T Ú x = y) & T & x ³ y =

= x ³ y

Следовательно, B₁ – это x ³ y и эскиз программы: ifx ³ y ® z := x fi

Чтобы не было авоста, нужен как минимум еще один предохранитель. Из теоремы: Q Þ B₁ Ú B₂. Другая возможность получить R - выполнить x := y. Рассуждая аналогично, получим: В₂ это y ³ x .

В результате: ifx ³ y ® z := x

y ³ x ® z := y

Поскольку ( x ³ y Ú y ³ x) = T (тождественно истина), то авоста не будет.

При x = y программа недетерминированная.

4. Оператор цикла whileBdoS: его семантика описывается с помощью инварианта цикла – предиката, истинного перед входом в цикл и после каждого выполнения тела цикла, в том числе в момент его завершения. Завершаемость, т.е. конечное число повторений цикла, описывается отдельным условием – целочисленной ограничивающей функцией.

В упрощенном виде основная теорема для цикла:

Если P & B Þwp (S, P), то P Þ wp (whileB doS, P & ù B) (если цикл завершается).

Пример инварианта - для цикла суммирования массива из 10 элементов b[i]

i:= 1; S:= b[0];

{ P }

whilei < 10 doS:= S + b[i]; i:= i + 1 od{ P };

{R : S = S (k=0, 9) b[k] }

Инвариант P : 1 £ i £10 & S = S (k=0, i-1) b[k]

т.е., на i-ом повторении цикла S - частичная сумма первых i элементов массива.

То, что неформально понимается программистом, здесь получает строго формальное выражение. Рекомендуется инвариант цикла строить до построения самого цикла.

(Задание 3).

Трудности и ограничения метода:

· Доказательство громоздко – длиннее самой программы – и может содержать ошибки

· Семантику машинных операций (вв/вы, вызов подпрограмм) трудно описать на языке предикатов 1-го порядка

Не найдя применения для последовательных программ реальной сложности, формальная верификация развивается сейчас для таких параллельных и распределенных программ, как протоколы где вычисления сравнительно просты. Там используются специальные виды логики, например, темпоральная (временная) логика.

1. Д. Грис. Наука программирования. М, Наука, 1985.

Вопросы и задания

1. Перечислите типичный набор возможностей отладчика (например, в Visual Studio). В чем заключаются основная проблема использования отладчика для отладки время-зависимых программ ?

2. Найдите классы в пространстве исходных значений переменных к и j, соответствующие четырем возможным путям во фрагменте программы:

j < 10,

fl_min £ k £ fl_max

k > 2 ?

нет да

k < j ?

нет да

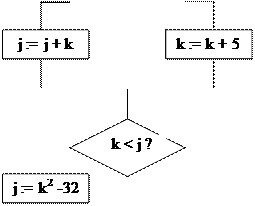Составьте логическую спецификацию программы, которая находит место максимального (по величине) элемента в массиве.

4. Напишите инвариант для цикла нахождения значения максимального элемента в массиве.

Задачи для дифференциальных уравнений в частных производных имеют очень большую область приложений. Вопросы существования и единственности решения исследуются в математической физике. Предметом вычислительной математики является получение приближенных решений этих задач сеточными методами, методом прямых, методом конечных элементов и другими методами. . В данной главе будут рассмотрены сеточный метод и метод прямых.