Дифференциальные зависимости между продольной силой и интенсивностью распределенной нагрузки.

В случае ЦР применим принцип Сен-Венана.

 

Пример 2.1 Определение внутренних усилий при растяжении и сжатии.

Рис. 2.3 Определение продольной силы на участках стержня.

Первый участок. (Рис. 2.3б)

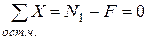
Второй участок. (Рис. 2.3в)

 

Рис. 2.4 Эпюра продольных сил.

Рис. 2.5 Вывод дифференциальной зависимости между t_x и N.

Сумма проекций всех сил, приложенных к элементу, на ось стержня:

(2.2)

Пример 2.2 Эпюра продольных сил для стержня переменного сечения от действия собственного веса.

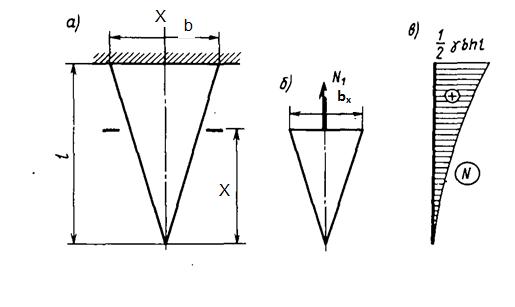
Рис. 2.6 Эпюра продольных сил.

Закон изменения продольной силы и ее производной

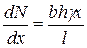
(2.3)

2.3 Закон Гука при растяжении и сжатии.

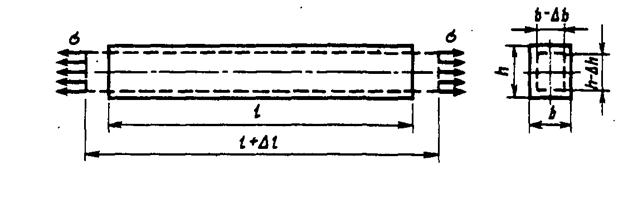
Рис. 2.7 Продольные и поперечные деформации стержня.

абсолютная продольная деформация	относительная продольная деформация	относительная поперечная деформация	относительная поперечная деформация

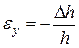
Закон Гука (упругая работа материала).

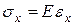
(2.4)

2.4 Обобщенный закон Гука.

Рис 2.8 Трехосное растяжение элемента

Рис. 2.9 Деформации элемента при растяжении его вдоль оси x.

Деформации элемента при растяжении его вдоль осей x,y,z.

Вдоль оси x
Вдоль оси y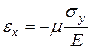
Вдоль оси z

Формулы обобщенного закона Гука.

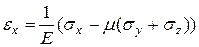
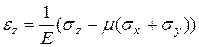
(2.5)

Относительное изменение объема параллелепипеда.

(2.6)

Вывод формулы:

(2.7)