Решение.
Построим таблицу значений факторной переменной 
и результативной переменной Y=q/A, а также расчетную таблицу:
| t | X | У | XУ | Х2 | У2 |
| 1,193 9 | 0,735 | 0,877 517 | 1,425 397 | 0,540 225 | |
| 1,203 0 | 0,737 | 0,886 611 | 1,447 209 | 0,543 169 | |
| 1,187 8 | 0,734 | 0,871 845 | 1,410 869 | 0,538 756 | |
| 1,131 4 | 0,716 | 0,810 082 | 1,280 066 | 0,512 656 | |
| 1,098 6 | 0,710 | 0,780 006 | 1,206 922 | 0,504 100 | |
| 1,054 3 | 0,699 | 0,736 956 | 1,111 548 | 0,488 601 | |
| 1,000 6 | 0,687 | 0,687 412 | 1,001 200 | 0,471 969 | |
| 0,996 9 | 0,686 | 0,683 873 | 0,993 810 | 0,470 596 | |
| 1,022 5 | 0,692 | 0,707 570 | 1,045 506 | 0,478 864 | |
| 0,978 3 | 0,683 | 0,668 179 | 0,957 071 | 0,466 489 | |
| ВСЕГО | 10,867 3 | 7,079 | 7,710 051 | 11,879 598 | 5,015 425 |
| СРЕДНЯЯ | 1,086 73 | 0,707 9 | 0,771 005 1 | 1,187 959 8 | 0,501 542 5 |
| t |
У=  +bХ
| e=У-У | e2 |
(У-  )2
| |
| 0,734 506 | 0,000 500 | 0,000 000 25 | 0,000 708 | ||
| 0,736 735 | 0,000 265 | 0,000 000 07 | 0,000 831 | ||
| 0,733 011 | 0,000 989 | 0,000 000 97 | 0,000 631 | ||
| 0,719 193 | -0,003 193 | 0,000 010 20 | 0,000 128 | ||
| 0,711 157 | -0,001 157 | 0,000 001 39 | 0,000 015 | ||
| 0,700 304 | -0,001 304 | 0,000 001 70 | 0,000 058 | ||
| 0,687 147 | -0,000 147 | 0,000 000 02 | 0,000 431 | ||
| 0,686 241 | -0,000 241 | 0,000 000 06 | 0,000 461 | ||
| 0,692 513 | 0,000 513 | 0,000 000 26 | 0,000 237 | ||
| 0,681 684 | 0,001 317 | 0,000 001 73 | 0,000 687 | ||
| ВСЕГО | 0,000 016 65 | 0,004 187 | |||
| СРЕДНЯЯ | 0,000 001 665 | 0,000 418 7 |
1) Найдем коэффициенты уравнения линии регрессии
Y=a+bX,
где дисперсии переменных X и Y равны
1,187 959 8 - (1,086 73)2 = 0,006 977 7
0,000 420 09,
а ковариация переменных X и Y равна
Cov(Х;У) = 
- 
× 
= 0,771 0 – 1,086 73 × 0,707 9 = 0,001708 8
b= 
0,245;
= 0,7079 – 0,245 × 1,08673 = 0,442.
Уравнение регрессии имеет вид
Y = 0,442 + 0,245X
2) Построим эмпирические точки и линию регрессии (постройте самостоятельно)
3) Найдем общую дисперсию, объясненную и необъясненную регрессией дисперсии по формулам:
общая дисперсия
= D(y) = 
- ( )2 = 0,501 542 5 - (0,7079)2 = 0,000 420 09
необъясненная регрессией часть дисперсии
× 0,000 016 65 = 0,000 001 665
объясненная регрессией часть дисперсии
×0,004 187 = 0,000 418 7
4) Найдем дисперсии D( ) и D(b) для оценок коэффициентов регрессии:
- несмещенная оценка дисперсии ошибок 
2
0,000 002 08
D(b) = Sb2 = 
= 
= 0,000 030
D( ) = S 
= 
×D(b) = 1,187 959 8 × 0,000 030 = 0,000 035
S 
= 0,005 951 u S в= 0,005 477 - средние квадратические отклонения оценок
5)Найдем коэффициент детерминации
1 - 
= 0,996 037
Значит, на 99,6 % изменения значений результативной переменной Y объясняется влиянием
факторной переменной X .
Коэффициент корреляции найдем по формуле:
,
где
0,083 533; 
0,020 496; cov(Х;У) = 0,001 708 8;
R= 
=0,998 016
Поскольку 0,7 <R< 1, то связь между значениями X и Y тесная.
Поскольку R > 0, то связь между Х и У прямая: с ростом значений Х средние значения У возрастают.
6) Проверим значимость коэффициентов регрессии. Для этого
а) проверим нулевую гипотезу Н: b=0 на уровне доверия 95%
Используя t-статистику получим
t = 
= 
= 
= 
= 44,733
Критическое значение tc = t(n-k) найдем по таблицам распределения Стьюдента при 
= 0,95 и n=10 – 2 = 8 (10 – количество наблюдений переменных Х и У)
tc = 2,306
Поскольку 
= 44,733 > tc = 2,306, то гипотеза Н: 
=0 о том, что между величинами Х и У нет линейной зависимости, должна быть отвергнута на уровне доверия 95%.
б) Проверим нулевую гипотезу Н: =0
Используя t-статистику получим
t = 
= 
= 
= 
= 74,27
Критическое значение статистики при a = 0,95 и n = 10 – 2 = 8 равно
tc = 2,306
Поскольку = 74,27 > tc = 2,306, то гипотеза Н: =0 должна быть отвергнута на уровне доверия 95%, т.е. с вероятностью 95 % можно утверждать, что 
0
6) Проверим гипотезу о значимости линейной регрессии с помощью F – статистики.
F = 
= 
= 
= 2013,6
(Можно F рассчитать по другой формуле:
F = 
× 
= 
× 
= 4024,258
Критическое значение статистики на 95 % уровне доверия находим по таблице распределения Фишера:
Fc = F(k-1; n-k) = F(1; 8) = 5,32
Поскольку F > Fc, 
то гипотеза Н: =0 отвергается и принимается альтернативная гипотеза Н1: 0 на уровне доверия 95%, т.е. модель значима.
8 а) Найдем доверительный интервал для на уровне доверия 95%. Для этого рассчитаем значение t-статистики
t = = 
Критическое значение tc найдем по таблицам распределения Стьюдента при = 0,95 и n=10–2 = 8
tc = 2,306
Решая неравенство < tc = 2,306 получим:
< 2,306
< 2,306 ×0,005477
0,245 - 0,013 < < 0,245 + 0,013
0,232 < < 0,258
С вероятностью 95% можно утверждать, что значение параметра лежит в промежутке
(0,232; 0,258)
б) Найдем доверительный интервал для на уровне доверия 95%. Для этого рассчитаем значение t-статистики
t = == 
Критическое значение tc найдем по таблицам распределения Стьюдента при = 0,95 и n = 10 – 2 = 8
tc = 2,306
Решая неравенство < tc = 2,306 получим:
< 2,306
< 2,306 × 0,005951
0,442 - 0,014 < < 0,442 + 0,014
0,428 < < 0,456
С вероятностью 95% можно утверждать, что значение параметра лежит в промежутке
(0,428; 0,456)
Задача 2. Построить статистическую модель
ln q =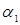 
+ 
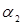ln A + 
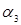ln k (У= ln q; Х 
= ln A; X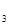 
= ln k)
и
1) найти уравнение регрессии;
2) найти объясненную и необъясненную регрессией дисперсии;
3) найти коэффициент детерминации и скорректированный коэффициент корреляции;
4) найти частные коэффициенты корреляции.
5) проверить гипотезы о незначимости коэффициентов модели
6) проверить гипотезу о незначимости регрессии в целом.
7) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
8) проверить наличие мультиколлинеарности.
Сделать выводы.