Решение СЛУ методом Зейделя

При решении СЛУ методом простой итерации каждый шаг итерационного процесса состоит в переходе от уже имеющегося приближения значений неизвестных к новому приближению.

Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении значений y_i учитываются уже полученные значения y₁, y₂,…,y_i-1.

I. Условие α<1 является достаточным для сходимости итерационного процесса метода Зейделя. Причем метод Зейделя обеспечивает более быструю сходимость, чем метод простой итерации.

Рассмотрим решение системы трех линейных уравнений с тремя неизвестными методом Зейделя (взяв за основу метод итерации)

program slu_zejdel1;

{ *** с использованием евклидовой метрики *** }

var p,b,x1,x2,x3,y1,y2,y3,a,e: real;

N: integer;

begin

write('Введите x1, x2, x3 : '); readln(x1,x2,x3);

write('Введите A, E : '); readln(a,e);

b:=e*(1-a)/a;

N:=0; {число итераций}

repeat

N:=N+1;

y1:= 0.1362*x2-0.1790*x3+16.1433;

y2:=-0.2238*y1+0.0909*x3+25.3154;

y3:= 0.1739*y1+0.2875*y2+21.3777;

p:=sqrt(sqr(x1-y1)+sqr(x2-y2)+sqr(x3-y3));

x1:=y1; x2:=y2; x3:=y3;

until p<=b;

writeln('x1 = ',x1:8:6);

writeln('x2 = ',x2:8:6);

writeln('x3 = ',x3:8:6);

writeln('Число итераций - N = ',N);

readln

end.

 

Введите x1, x2, x3 : 0 0 0

Введите A, E : 0.2218 0.0001

x1 = 13.999370

x2 = 25.000219

x3 = 30.999753

Число итераций - N=6

 

Как видно из примера, по сравнению с методом итераций решение получено за меньшее количество шагов.

 

II. Рассмотрим практическую схему преобразования исходной СЛУ, гарантирующую сходимость метода Зейделя.

Пусть система записана в матричной форме: Ax=b.

Умножим левую и правую части слева на матрицу A^T: A^TAx= A^T b.

Обозначим : A^TA=C, A^T b=d.

Преобразованная система станет иметь вид: Cx=d. Такую систему называют нормальной:

· матрица C является симметричной;

· все элементы главной диагонали матрицы C положительны.

Нормальную систему легко привести к виду:

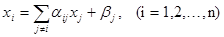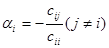, где и .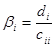

Вычислительные формулы имеют вид:

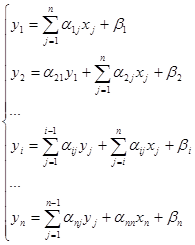
Рассмотрим на примере.

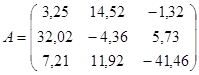
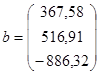
После деления на диагональные элементы получим:

Рассмотрим решение системы трех линейных уравнений с тремя неизвестными методом Зейделя (взяв в качестве метрики, используемой в программе, ).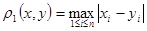

program slu_zejdel2;

var x1,y1,x2,y2,x3,y3,e,a,b,c: real;

N: integer;

begin

write('Введите X1, X2, X3 - '); readln(x1,x2,x3);

write('Введите погрешность Е - '); readln(e);

N:=0; {число итераций}

repeat

N:=N+1;

y1:= 0.0060*x2+0.1101*x3+10.4389;

y2:= 0.0174*y1+1.4475*x3-20.1153;

y3:= 0.0683*y1+0.3070*y2+22.3686;

a:=abs(y1-x1); b:=abs(y2-x2); c:=abs(y3-x3);

if a<b then a:=b;

if a<c then a:=c;

x1:=y1; x2:=y2; x3:=y3;

until a<=e;

writeln('X1 = ',x1:11:8);

writeln('X2 = ',x2:11:8);

writeln('X3 = ',x3:11:8);

writeln('Число итераций - N = ',N);

readln

end.

 

Введите X1, X2, X3 - 0 0 0

Введите погрешность Е - .0001

X1 = 14.00204110

X2 = 25.00128107

X3 = 31.00033269

Число итераций - N = 18