Метод половинного деления

Уточнение корней

Уточнение корней может осуществляться различными методами.

Пусть 1) функция y=F(x) определена и непрерывна на отрезке [a,b].

2) F(a)F(b)<0

Требуется найти корень на отрезке с точностью ε.

Разделим отрезок [a,b] пополам точкой 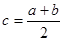. Если 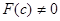, то возможны два случая: 1) F(x) меняет знак на отрезке [a; c];

2) F(x) меняет знак на отрезке [c; b].

Выбираем тот отрезок, на котором функция меняет знак. Если F(x) меняет знак на отрезке [a; c], то b:=c; если F(x) меняет знак на отрезке [c; b], то a:=c.

Условие окончания счета: .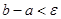

Корень уравнения: 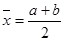. Погрешность метода: .

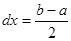Рассмотрим положительные и отрицательные стороны метода половинного деления.

«Плюсы»:	«Минусы»:
· надежность · не требует приведения к специальному виду · не требует дифференцируемости функции · устойчив к ошибкам округления	· медленная сходимость · метод не применим для корней четной кратности:

 

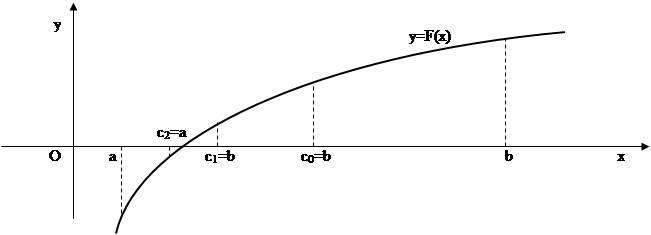
Программа уточнения корней методом половинного деления:

program pol_del;

var a,b,c,e,x,dX: real;

N:integer;

function f(x: real):real;

begin

{записать, функцию в виде f:=[математическое выражение]}

f:=x*x*x-x+4;

end;

begin

write('Введите левую границу отрезка - a: ');readln(a);

write('Введите правую границу отрезка - b: ');readln(b);

write('Введите требуемую погрешность - e:'); readln(e);

N:=0;

repeat N:=N+1; c:=(a+b)/2;

if f(a)*f(c)<0 then b:=c else a:=c;

until b-a<e;

x:=(a+b)/2; dX:=(b-a)/2;

writeln('Приближенное значение корня - Х = ',x);

writeln('Ошибка не превышает dX = ',dX);

writeln('Число итераций - N = ',N);

readln

end.

Блок-схема уточнения корней методом половинного деления:	Результаты выполнения программы:
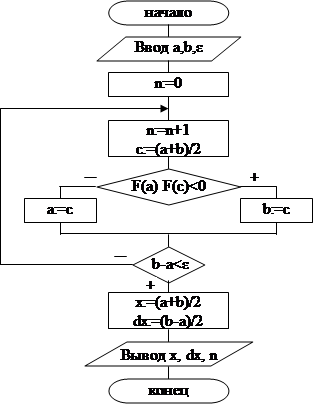
	Введите левую границу отрезка - a: -2 Введите правую границу отрезка - b: -1 Введите требуемую погрешность - e:.0001 Приближенное значение корня - Х = -1.7962951660E+00 Ошибка не превышает dX = 3.0517578125E-05 Число итераций - N = 14