Задания для контрольной работы

Белокопытов А. В.

 

 

Эконометрика

(задания для выполнения контрольных работ)

 

Смоленск – 2013


Контрольная работа состоит из 3 задач. Студент выбирает те номера задач, которые соответствуют двум последним цифрам шифра его зачетной книжки (варианты приведены в конце пособия на странице 56). Например, при шифре 23 необходимо решить задачи №8, 42, 65.

Условие и решение каждой задачи оформляется письменно в отдельной тетради. Работу необходимо аккуратно оформить, решения должны быть полными, без арифметических ошибок и недочетов.

Задания для контрольной работы

Задача 1. По 8 наблюдениям построена модель парной регрессии следующих функций:

у=а+b1x3; y=a+b/x; y=b1x+b2x4; y=a+b1x+b2/x.

Задание: Определить какие из построенных моделей точно будут статистически ненадежными.

Задача 2. По семи территориям за 2003 г. известны значения двух признаков:

Район Расходы на покупку продовольственных товаров в общих расходах, % Среднемесячная заработная плата одного работающего, руб.
68,8
61,2
59,9
56,7
55,0
54,3
49,3

Задание:

1.Определите факторный, результативный признаки и постройте уравнение линейной регрессии. Дайте интерпретацию его параметров.

2.Вычислите коэффициент детерминации через общую и факторную дисперсии, что показывает данный коэффициент.

Задача 3. Пусть имеется следующая модель регрессии, характеризующая зависимость у от x: ух = 8-7x. Известно также, что rxy= -0,5 ; n = 20.

Задание:

1. Постройте доверительный интервал для коэффициента регрессии в этой модели: а) с вероятностью 90%;

б) с вероятностью 99%.

2. Проанализируйте результаты, полученные в п.1, и поясните причины их различий.

Задача 4.Исследуя спрос на тракторы марки N, аналитический отдел тракторного завода по данным, собранным по 19 торговым точкам, выявил следующую зависимость: lnу =10,3 - 0,8 lnx,

(2,5) (-3,5)

где у - объем продаж тракторов марки N в отдельной торговой точке;

x - средняя цена трактора в данной торговой точке;

В скобках приведены фактические значения t-критерия Стьюдента для параметров уравнения регрессии.

Задание:

До проведения этого исследования администрация завода предполагала, что эластичность спроса по цене для тракторов марки N составляет -0,9. Подтвердилось ли предположение администрации результатами исследования?

Задача 5. По совокупности 30 предприятий торговли изучается зависи­мость между признаками: х - цена на товар А, тыс. руб.; у - прибыль торгового предприятия, млн руб. При оценке регрессионной модели были получены следующие промежуточные результаты: S(yi-yx)2 =39000; S(yi-`y )2=120000.

Задание:

1. Поясните, какой показатель корреляции можно определить по этим данным.

2. Постройте таблицу дисперсионного анализа для расчета значения F-критерия Фишера. Сравните фактическое значение F-критерия с табличным.

3. Сделай­те выводы.

Задача 6. Зависимость объема продаж у (тыс. руб.) от расходов на рекла­му х (тыс. руб.) характеризуется по 12 сельскохозяйственным предприятиям следующим образом:

Уравнение регрессии у=10,7+ 0,62х

Среднеквадратичное отклонение х sх =4,7

Среднеквадратичное отклонение у sу=3,4

Задание:

1. Определите коэффициент корреляции.

2. Оцените значимости уравнения регрессии в целом.

3. Найдите стандартную ошибку оценки коэффициента регрессии.

4. Оцените значимость коэффициента регрессии через t-критерий Стьюдента.

5. Определите доверительный интервал для коэффициента регрессии с вероятностью 0,95 и сделайте экономический вывод.

Задача 7. Исследуется зависимость объема производства продукции (у) от энергетических мощностей (х1), производственных фондов (х2) и цен на сырье (х3). Были получены следующие варианты уравнений регрессии:

ух = 12 + 2,1х1 + 5,3х2 - 7,2х3

(0,8) (4,1) (2,4)

ух =19 + 1,8х1+6,2х2

(0,4) (4,4)

ух =15 + 2,2х1 - 4,3х3

(0,7) (1,1)

В скобках указаны стандартные ошибки для коэффициентов регрессии.

Задание: Выберите наилучшее уравнение регрессии, обоснуйте принятое решение.

Задача 8.Изучается зависимость потребления материалов у от объема производства продукции х. По 20 наблюдениям были получены следующие варианты уравнения регрессии:

1. у =3+ 2 х

(6,48)

2. ln y=2,5+ 0,2 ln x, r2=0,68.

(6,19)

3. у=1,1+0,8 ln х, r2=0,69.

(6,2)

4. у=3+ l,5х + 0,1х2, r2=0,701

(3,0) (2,65)

В скобках указаны фактические значения t-критерия.

Задание:

1. Определите коэффициент детерминации для 1-го уравнения.

2. Запишите функции, характеризующие зависимость у от х во 2-м и 3-м уравнениях.

3, Определите коэффициенты эластичности для каждого из уравне­ний.

4. Выберите наилучший вариант уравнения регрессии.

Задача 9.Для трех видов продукции K, M и N модели зависимости удель­ных расходов от объема выпускаемой продукции вы­глядят следующим образом:

УK = 600,

у M = 80 + 0,7x,

уN = 40 х0,5

Задание:

1. Определите коэффициенты эластичности по каждому виду про­дукции и поясните их смысл.

2. Сравните при х = 1000 эластичность затрат для продукции M и N.

3. Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для продукции M и N были рав­ны.

Задача 10.По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от фак­торов, приведенных в таблице.

Признак-фактор Уравнение парной регрессии Среднее значение фактора
Объем производства, млн руб.,х1 ух = 0,63 + 59,3/х 2,66
Трудоемкость единицы продукции, чел-час, х2 ух = 9,28 + 9,91х2 1,41
Оптовая цена за 1 т. минеральных удобрений, тыс.руб., х3 ух=11,82+х31,57 1,51
Доля прибыли, изымаемой государством, %, х4 ух = 14,86 •1,017х4 26,3

Задание:

1. Определить с помощью средних коэффициентов эластичности силу влия­ния каждого фактора на результат.

2. Ранжировать факторы по силе влияния.

Задача 11.По 20 регионам страны изучается зависимость уровня безрабо­тицы у (%) от индекса потребительских цен х (% к предыдущему году). Информация о логарифмах исходных показателей представ­лена в таблице:

Показатель ln x ln у
Среднее значение 0,6 1,0
Среднее квадратическое отклонение 0,4 0,2

Известно также, что коэффициент корреляции между логариф­мами исходных показателей составил r lnx lny =0,8.

Задание:

1. Постройте уравнение регрессии зависимости уровня безработицы от индекса потребительских цен в степенной форме.

2. Дайте интерпретацию коэффициента эластичности данной модели регрессии.

return false">ссылка скрыта

3. Определите значение коэффициента детерминации и поясните его смысл.

Задача 12.Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам:

Показатель Материалоемкость продукции по заводам
Потребле­но мате­риалов на единицу продукции, кг 3,7 3,6 3,5 3,5
Выпуск продукции, тыс. ед.

Задание:

1.Найдите параметры уравнения у = a +b/x.

2.Оцените тесноту связи с помощью индекса корреляции.

3.Охарактеризуйте эластичность изменения материалоемкости про­дукции.

4.Сделайте вывод о значимости уравнения регрессии.

Задача 13.Зависимость спроса на товар К от его цены характеризуется по 20 наблюдениям уравнением: lg y = 1,75 -0,35 lgх. Доля остаточной дисперсии в общей составила 18%.

Задание:

1. Запишите данное уравнение в виде степенной функции.

2. Оцените эластичность спроса на товар в зависимости от его цены.

3. Определите индекс корреляции.

4. Оцените значимость уравнения регрессии через F-критерий Фишера. Сделайте выводы.

Задача 14.По группе 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции у (тыс. руб.) от уровня технической оснащенности х (тыс.руб.): у =19+650/х .

Доля остаточной дисперсии в общей составив 0,17.

Задание:

1. Определить коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.

2. Рассчитать индекс корреляции и F-критерий Фишера. Сделайте выводы.

Задача 15.Зависимость объема производства у (тыс. ед.) от численности занятых х (чел.) по 15 крестьянско-фермерским хозяйствам характеризуется следующим образом: уравнение регрессии у = 33 - 0,4х +0,05 х2 .

Доля остаточной дисперсии в общей 21%

Задание:

Определите:

а) индекс корреляции;

б) значимость уравнения регрессии;

в) коэффициент эластичности, предполагая, что численность занятых составляет 20 человек.

Задача 16.По 20 фермам области получена следующая информация:

Показатель Среднее значение Коэффициент вариации,%
Урожайность, ц/га
Внесено мин.удобрений на 1 га посева, кг

Фактическое значение F-критерия Фишера составило 44.

Задание:

1. Определите линейный коэффициент детерминации.

2. Постройте уравнение линейной регрессии.

3. Найдите обобщающий коэффициент эластичности.

4. С вероятностью 0,95 укажите доверительный интервал ожидаемого значения урожайности в предположении роста количества внесенных удобрений на 10% от своего среднего уровня.

Задача 17.Для двух видов продукции А и В зависимость производственных затрат предприятия у (тыс. руб.) от объема производства х (шт.) характеризуется данными, представленными в таблице.

Уравнение регрессии Показатели корреляции Число наблюдений
УА =160+0,8х 0,85
УВ=50х0,6 0,72

Задание:

1. Поясните смысл величин 0,8 и 0,6 в уравнениях регрессии.

2. Сравните эластичность расходов от объема производства для про­дукции А и В при выпуске продукции А в 500 единиц.

3. Определите, каким должен быть выпуск продукции А, чтобы эластичность ее расходов совпадала с эластичностью расходов на про­дукцию В.

4. Оцените значимость каждого уравнения регрессии с помощью F-критерия Фишера.

Задача 18. На основе квартальных данных с 1998 по 2003г. с помощью метода МНК получено следующее уравнение у от 3 факторов (в скобках указаны стандартные ошибки):

уt= 1,12 - 0,0098x1 - 5,62x2 + 0,044x3

(2,14) (0,0034) (3,42) (0,009)

Известно, что сумма квадратов отклонений S2факт= 110,32, S2ост == 21,43.

Задание:

1. Проверьте значимость каждого из коэффициентов.

2. Найдите коэффициент детерминации.

3. Протестируйте значимость регрессии в целом.

4. Когда в уравнение были добавлены три фиктивные переменные соответствующие трем первым кварталам года, величина S2факт выросла до 118,2. Проверьте гипотезу о наличии сезонности, сформулировав необходимые предположения о виде этой сезонно­сти.

Задача 19.По 20 предприятиям отрасли были получены следующие резуль­таты регрессионного анализа зависимости объема выпуска продук­ции у (млн руб.) от численности занятых на предприятии x1 (чел.) и среднегодовой стоимости основных фондов х2 (млн руб.):

Коэффициент детерминации 0,82
Множественный коэффициент корреляции ?
Уравнение регрессии lny = ?+ 0,46 ln x1+0,59 ln x2
Стандартные ошибки параметров 2 0,05 ?
t-критерий для параметров 5 ? 5

Задание:

1. Напишите уравнение регрессии, характеризующее зависимость у от х1 и x2.

2. Восстановите пропущенные характеристики.

3. С вероятностью 0,95 постройте доверительные интервалы для коэффициентов регрессии.

4. Проанализируйте результаты регрессионного анализа.

Задача 20.По 40 предприятиям одной отрасли исследовалась зависимость производительности труда - у от уровня квалификации рабочих – х1 и энерговооруженности их труда – х2. Результаты оказались сле­дующими:

Уравнение регрессии у= а + 14 х1 + 3 х2
Стандартные ошибки параметров 0,5 ?
t-критерий для параметров ?
Множественный коэффициент корреляции     0,85    

Задание:

1. Определите параметр а и заполните пропущенные значения.

2. Оцените значимость уравнения в целом, используя значение множественного коэффициента корреляции.

3. Какой из факторов оказывает более сильное воздействие на ре­зультат?

Задача 21.По 30 предприятиям отрасли были получены следующие резуль­таты регрессионного анализа зависимости объема выпуска продук­ции у (млн руб.) от численности занятых на предприятии х1 (чел.) и среднегодовой стоимости основных фондов х2 (млн руб.):

Коэффициент детерминации ?
Множественный коэффициент корреляции 0,87
Уравнение регрессии y = ?+ 0,56 x1+20 x2
Стандартные ошибки параметров 4 0,07 ?
t-критерий для параметров 3 ? 4

Задание:

1. Восстановите пропущенные характеристики.

2. С вероятностью 0,95 постройте доверительные интервалы для коэффициентов регрессии.

3. Проанализируйте результаты регрессионного анализа.

Задача 22.По данным, полученным от 20 фермерских хозяйств одного из регионов, изучается зависимость объема выпуска продукции расте­ниеводства у (млн руб.) от трех факторов: численности работников L (чел.), количества минеральных удобрений на 1 га посева М (кг) и количества осадков в период вегетации - R (г). Были получены сле­дующие варианты уравнений регрессии и доверительные интервалы для коэффициентов регрессий:

l) y = -5+0,8L+l,2M, R2 =0,75.

Граница Доверительные интервалы для коэффициентов регрессии при факторе
L М
Нижняя 0,4 ?
Верхняя ? 1,4
Примечание. Доверительные интервалы построены с вероятностью a = 0,05.

2) y=2+0,5L+1,7M-2R, R2 =0,77.

Граница Доверительные интервалы для коэффициентов регрессии при факторе
L М R
Нижняя 0,1 ? ?
Верхняя ? 2,3 1,5
Примечание. Доверительные интервалы построены с вероятностью a = 0,05.

Задание:

1. Восстановите пропущенные границы доверительных интервалов в каждом уравнении.

2. Выберите наилучшее уравнение регрессии. Дайте интерпретацию их параметров и доверительных интервалов для коэффициентов рег­рессии.

3. Каковы ваши предложения относительно значения t-критерия Стьюдента для коэффициента регрессии при факторе R во 2-м урав­нении?

Задача 23.По данным, полученным от 20 фермерских хозяйств одного из регионов, изучается зависимость объема выпуска продукции расте­ниеводства y (млн руб.) от четырех факторов: численности работни­ков L (чел.), количества минеральных удобрений на 1 га посева М(кг), количества осадков в период вегетации R (г) и качества поч­вы Q (баллов). Были получены следующие варианты уравнений регрессии и доверительные интервалы коэффициентов регрессий:

1) y=2+0,5L+l,7M-2R, R2 =0,77.

Граница Доверительные интервалы для коэффициентов регрессии при факторе
L М R
Нижняя 0,1 ? ?
Верхняя ? 2,3 1,5
Примечание. Доверительные интервалы построены с вероятностью a = 0,05.

2) y=6,4+0,7L+l,5M-2R+0,8Q, R2 =0,81.

Граница Доверительные интервалы для коэффициентов регрессии при факторе
L М R Q
Нижняя 0,3 -0,2 ? 0,4
Верхняя ? ? -1,2 1,2
Примечание. Доверительные интервалы построены с вероятностью a = 0,05.

Задание:

1. Восстановите пропущенные границы доверительных интервалов.

2. Выберите наилучшее уравнение регрессии. Дайте интерпретацию его параметров и доверительных интервалов для коэффициентов регрессии на примере одного из факторных признаков.

3. Оцените целесообразность включения в модель у =f(L, М, R) фак­тора Q.

Задача 24.По 50 семьям изучалось потребление мяса - у (кг на душу насе­ления) от дохода – x1 (руб. на одного члена семьи) и от потребления рыбы – x2 (кг на душу населения). Результаты оказались следующими:

Уравнение регрессии y=-180+0,2x1 –0,4x2
Стандартные ошибки параметров 20 0,01 0,25
Множественный коэффициент корреляции 0,85

Задание:

1. Используя t-критерий Стьюдента, оцените значимость параметров уравнения.

2. Рассчитайте F-критерий Фишера.

3. Оцените по частным F-критериям Фишера целесообразность включения в модель: фактора х1 после фактора x2, фактора х2 после фактора x1.

Задача 25. Зависимость спроса на свинину х1 от цены на нее х2 и от цены на говядину х3 представлены уравнением lg x1=0,12-0,22*lg x2+2,73*lg x3.

Задание:

1. Представить данное уравнение в естественной форме.

2. Оценить значимость параметров данного уравнения, если известно, что t- критерий для параметра b2 при x2 составил 0,81, а для параметра b3 при х3 –1,01.

3. Сделайте выводы о возможности использования уравнения для прогноза.

Задача 26. По 19 предприятиям оптовой торговли изучается зависимость объема реализация (у) от размера торговой площади (х1) и товарных запасов (х2). Были получены следующие варианты уравнения регрессии:

1.y=25+15x1 r2=0,9;

2. y= 42+27x2 r2=0,84;

3. y= 30+ 10x1+8x2 R2=0,92;

(2,5) (4,0)

4.y=21 + 14x1 + 20x2 + 0,6x22 R2=0,95.

(5,0) (12,0) (0,2)

В скобках указаны значения стандартных ошибок для коэффициентов регрессии.

Задание:

1. Проанализируйте тесноту связи результата с каждым из факторов.

2. Выберите лучшее уравнение регрессии, обоснуйте свое решение.

Задача 27. В результате исследования факторов, определяющих рост объема продукции (у) по 73 хозяйствам получено следующее уравнение регрессии:

у=1,4 - 0,52х1 + 0,17х2 + 11,16х3 - 0,38х4 - 4,75х5, R2=0,6

(-5,9) (4,34) (3,91) (-0,79) (-2,7)

Задание:

1. Проверьте гипотезу о достоверности полученной модели в целом.

2. До получения результатов этого исследования ваш однокурсник заключил с вами пари, что аналитические результаты по данной модели докажут наличие обратной связи между у и х4. Выиграл ли ваш однокурсник?

Задача 28.Производственная функция, полученная по данным за 1990 -1997 гг., характеризуется уравнением

lg V =0,552 + 0,276×1g P+ 0,521×1g К , R2 = 0,984 , r2VP = 0,7826, r2VK = 0,9836.

(0,584) (0,065)

где V - индекс промышленного производства; P - численность рабочих; К - капитал.

В скобках указаны значения стандартных ошибок для коэффициентов рег­рессии.

Задание:

1. Дайте интерпретацию параметров уравнения регрессии.

2. Оцените значимость параметров регрессии с помощью t-критерия Стьюдента и сделайте соответствующие выводы о целесообразности включения факторов в модель.

3. Оцените значимость уравнения регрессии в целом с помощью F-критерия Фишера.

4. Найдите величины частных значений F-критерия и сделайте соот­ветствующие выводы.

5. Какова роль факторов, не учтенных в модели, в вариации индекса промышленного производства.

Задача 29. Для проверки гипотезы о том, что производительность труда у в сельском хозяйстве зависит от уровня зарплаты х, была получена регрессия: ln у =0,297+0,613х , R2=0,93

(0,038)

В скобках указана стандартная ошибка коэффициента регрессии.

Задание:

1. Проверить гипотезу о значимости уравнения в целом.

2. Было высказано предположение, что приведенное выше уравнение содержит ошибки спецификации, поскольку оно не учитывает уровень технической оснащенности, оказывающий сильное влияние на производительность труда и положительно коррелированный с зарплатой. Как это предположение повлияет на ваш вывод?

Задача 30. Бюджетное обследование пяти случайно выбранных семей дало следующие результаты (в млн.руб.):

Семья Накопления, у Доход, х1 Имущество,х2

1 3 40 60

2 6 55 36

3 5 45 36

4 3.5 30 15

5 1.5 30 90

Задание:

1. Оцените линейную регрессию у на х1 и х2.

2. Спрогнозируйте накопления семьи, имеющей доход 40 млн.руб. и имущество стоимостью 25 млн. руб.

3. Предположим, что доход семьи возрос на 10 млн. руб., в то время как стоимость имущества не изменилась. Оцените, как возрастут её накопления.

4. Оцените, как возрастут накопления семьи, если её доход вырос на 5 млн. руб., а стоимость имущества увеличилась на 15 млн. руб.

5. Найдите сумму квадратов остатков и оценку остаточной дисперсии.

Задача 31. По 30 наблюдениям получены следующие данные:

Уравнение регрессии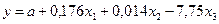
Коэффициент детерминации 0,65

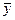
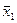
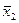
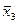
Задание: Найдите скорректированный коэффициент корреляции, оцените значимость уравнения регрессии в целом.

Задача 32.По совокупности 30 предприятий изучается зависимость прибыли y (тыс.руб.) от выработки продукции на одного работника 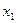(ед.) и индекса цен на продукцию (%):

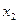Признак Среднее значение Среднее квадратическое отклонение Парный коэффициент корреляции
y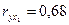

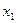
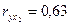
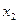
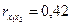
Задание:

1. Найти линейное уравнение множественной регрессии в стандартизированной форме.

2. Определить силу влияния каждого фактора.

3. Рассчитать показатель множественной корреляции и детерминации.

Задача 33. Изучается влияние размера стоимости основных и оборотных средств на величину валового дохода торгового предприятия, характеризующееся данными, приведенными в таблице.

Номер предприятия Валовой доход за год, млн. руб. Среднегодовая стоимость, млн. руб.
основных фондов оборотных средств
         

Задание: Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделайте выводы.

Задача 34. Изучалась зависимость вида 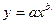. Для преобразованных в логарифмах переменных получены следующие данные:

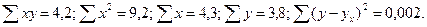
Задание:

1. Найдите параметры а и b.

2. Найдите показатель корреляции и оцените его значимость, если .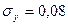

3.Оцените значимость уравнения, если известно, что n=9.

Задача 35.Для трех видов продукции А, В и С модели зависимости удель­ных постоянных расходов от объема выпускаемой продукции вы­глядят следующим образом: уA = 550, у B = 80 + 0,7x, уC = 40 х0,5 .

Задание:

1. Определите коэффициенты эластичности по каждому виду про­дукции и поясните их смысл.

2. Сравните при х = 1000 эластичность затрат для продукции В и С.

3. Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для продукции В и С были рав­ны.

Задача 36.По 30 наблюдениям получены следующие данные:

уравнение регрессии y=a+0,23x1+0,03x2-9,15x3
коэффициент детерминации 0,68
`у
`х1
`х2
`х3

Задание:

1. Найдите скорректированный коэффициент корреляции, оцените значимость уравнения регрессии в целом.

2. Определите частные коэффициенты эластичности.

3. Оцените параметр а.

Задача 37.Зависимость среднемесячной производительности труда от воз­раста рабочих характеризуется моделью: у = а + bx + сх2 . Ее исполь­зование привело к результатам, представленным в таблице.

№ п/п Производительность труда рабочих, тыс. руб., у № п/п     Производительность труда рабочих, тыс. руб., у
фактиче­ская расчетная фактиче­ская расчетная

Задание:Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.

Задача 38.Моделирование прибыли фирмы по уравнению у = abx привело к результатам, представленным в таблице.

№ п/п Прибыль фирмы, тыс. руб., у № п/п     Прибыль фирмы, тыс. руб., у
фактиче­ская расчетная фактиче­ская расчетная

Задание:

a) определите ошибку аппроксимации;

б) найдите показатель тесноты связи прибыли с исследуемым в мо­дели фактором;

в) рассчитайте F-критерий Фишера. Сделайте выводы.

Задача 39. Для изучения рынка жилья в городе по данным о 46 коттеджах было построено уравнение множественной регрессии:

y=19,3 - 5,9x1 + 0,96x2 + 3,43x3 ; R2=0,68,

(1,7) (0,53) (0,77)

где у- цена объекта, тыс.долларов; х1- расстояние до центра города, км; х2- полезная площадь объекта, кв. м; х3- число этажей в доме, ед.

В скобках указаны значения стандартных ошибок для коэффициентов мно­жественной регрессии.

Задание:

1. Проверьте гипотезу о том, что коэффициент регрессии b1 в генеральной совокупности равен 0.

2. Проверьте гипотезу о том, что коэффициент регрессии b2 генеральной совокупности равен 0.

3. Проверьте гипотезу о том, что коэффициент регрессии b3 в генеральной совокупности равен 0.

4. Проверьте гипотезу о том, что коэффициенты регрессии b1, b2 и b3 в генеральной совокупности одновременно равны 0.

5. Поясните причины расхождения результатов, полученных в пп. 1, 2 и 3, с результатами, полученными в п. 4.

Задача 40. По 20 предприятиям пищевой промышленности получена следующая информация, характеризующая зависимость объема выпуска продукции у (млн.руб.) от количества отработанных за год чел.- час х1(тыс. чел-ч.) и среднегодовой стоимости производственного оборудования х2 (млн. руб. ):

уравнение регрессии y=33 + 0,07 x1 + 2,4 x2
множественный коэффициент корреляции 0,9
сумма квадратов отклонений расчетных значений результата от фактических

Задание:

1. Определите коэффициент детерминации в этой модели (нескорректи­рованный и скорректированный).

2. Рассчитайте факторную дисперсию, приходящуюся на одну степень свободы, и оцените значимость уравнения в целом.

3. Какова роль факторов, неучтенных в модели.

Задача 41. Строится регрессия y=f(x1,x2,…xp) и вычисляется коэффициент детерминации R21. Затем в модель добавляется еще один фактор xp+1 и вычисляется коэффициент детерминации R22. Получилось, что R21= R22 . Что это означает?

Задача 42. В таблице представлены данные по реальному доходу на душу населения у (тыс.долл.), проценту рабочей силы, занятой в сельском хозяйстве х1 и среднему уровню образования населения в возрасте после 25 лет х2 (число лет, проведенных в учебных заведениях) для развитых стран.

№ страны у х1 х2 № страны у х1 х2
       

Задание:

1. Постройте множественную регрессию у от х1 и х2. Интерпретируйте полученные результаты.

2. Определите коэффициенты эластичности.

3. Почему, как правило, константа а не играет существенной роли при рассмотрении надежности регрессии?

4. Постройте 95% доверительные интервалы для коэффициентов регрессии.

5. Вычислите коэффициент детерминации (нескорректи­рованный и скорректированный).

6. Проверьте на 5% уровне значимость коэффициентов b1 и b2.

Задача 43. Анализируется зависимость объема производства сельскохозяйственной продукции от затрат труда и рас­хода кормов. Для этого по 20 предприятиям собраны следую­щие данные: у - объем продукции предприятия в среднем за год (млн руб.), x1 - среднегодовая списочная численность рабочих пред­приятия (чел.), х2 - средние затраты кормов в год в расчете на 1 условную голову (к.ед.). В результате корреляционного анализа получены матрицы парных коэффициентов корреляции.

для исходных переменных для натуральных логарифмов исходных переменных
  у х1 х2   ln y x1 x2
y 1,00     ln y 1,00    
x1 0,78 1,00   ln x1 0,86 1,00  
x2 0,86 0,96 1,00 ln x2 0,90 0,69 1,00

Задание:

1. Поясните смысл приведенных выше коэффициентов.

2. Используя эту информацию, опишите ваши предположения отно­сительно:

а) знаков коэффициентов регрессии в уравнениях парной линей­ной регрессии у по х1 (y=a+b x1) и у по х2 (y=а+bх2);

б) статистической значимости коэффициентов регрессии при пе­ременных x1 и x2 в линейном уравнении множественной регрессии и в уравнении множественной регрессии в форме функции Кобба -Дугласа.

3. Определите значения коэффициентов детерминации в уравнениях парной линейной регрессии y=a+bх1 и y=a+bx2 . Какое из этих уравнений лучше?

4. Определите частные коэффициенты корреляции для линейного уравнения множественной регрессии.

5. Найдите уравнение множественной линейной регрессии в стан­дартизованном масштабе и сделайте выводы.

Задача 44.Имеетсяинформация по 25 наблюдениям.

Признаки Среднее значение Коэффициент вариации, % Уравнение регрессии
У у = 20 + 1,1 x1 - 2,3x2
х1 у = 9,2 +1,3x1
x2 у =5 - 4,2 x2

Задание:

1. Оцените значимость каждого уравнения регрессии, если известно, что rx1 x2 = -0,35.

2. Оцените значимость коэффициентов регрессии уравнения с двумя объясняющими переменными.

3. Определите показатели частной корреляции.

4. Найдите частные средние коэффициенты эластичности.

Задача 45.По совокупности 30 предприятий изучается зависи­мость прибыли у (тыс. руб.) от выработки продукции на одного ра­ботника x1 (ед.) и индекса цен на продукцию х2 (%).

Признак Среднее значение Среднее квадратическое отклонение Парный коэффициент корреляции
У ry x1 = 0,71
х1 ry x2 =0,61
x2 rx1 x2=0.44

Задание:

1. Постройте линейные уравнения парной регрессии, оцените их значимость с помощью F-критерия Фишера.

2. Найдите уравнение множественной регрессии в стандартизован­ном и натуральном масштабе.

3. Рассчитайте множественный коэффициент корреляции, общий и частные критерии Фишера и сделайте выводы.

Задача 46.Зависимость потребления электроэнергии (тыс. кBт ч) от объ­емов производства продукции А – x1 (тыс. ед.) и продукции Б – x2 (тыс. ед.) характеризуется следующим образом:

уравнение регрессии в стандартизированном виде ty=0,79tx1 +0,56tx2
коэффициент детерминации 0,95
коэффициент вариации у, Vy 27%
коэффициент вариации х1 , Vx1 45%
коэффициент вариации х2 , Vx2 40%

Задание:

1. Сделайте выводы о силе влияния факторов на результат.

2. Учитывая значения коэффициентов вариации рассматриваемых признаков, определите частные коэффициенты эластичности, сде­лайте по ним выводы.

3. Оцените значимость уравнения регрессии, учитывая, что оно по­строено по 30 наблюдениям.

Задача 47.По 30 заводам, выпускающим продукцию А, изучается зависи­мость потребления электроэнергии у (тыс. кВт • ч) от производства продукции – x1 (тыс. ед.) и уровня механизации труда – х2 (%).

Признак Среднее значение Среднее квадратическое отклонение Парный коэффициент корреляции
У ry x1 = 0,77
Х1 ry x2 =0,43
X2 41,5 rx1 x2=0.38

Задание:

1. Постройте уравнение множественной регрессии в стандартизо­ванном и натуральном масштабе.

2. Определите показатели частной и множественной корреляции.

3. Найдите частные коэффициенты эластичности и сравните их с b-коэффициентами.

4. Рассчитайте общий и частные F-критерии Фишера.

Задача 48. По 30 территориям России имеются данные, представленные в таблице.

Признаки Среднее значение Среднее квадратическое отклонение Линейный коэффициент парной корреляции
Среднедневной душевой доход, руб., y 86,8 11,44 -
Среднедневная заработная плата одного работающего, руб., 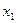54,9 5,86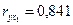
Средний возраст безработного, лет, 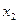33,5 0,58 ryx2=-0,210

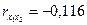
Задание:Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.

Задача 49. По 25 предприятиям изучается зависимость производительность труда у (тыс.руб.) от энерговооруженности труда x1 (кВт • ч на одного рабочего) и фондовооруженности x2 (тыс. руб.).

Признаки Среднее значение Среднее квадратическое отклонение Парный коэффициент корреляции
У 32,0 6,0 ry x1 = 0,52
Х1 4,3 0,5 ry x2 =0,84
X2 100,0 rx1 x2=0,43

Задание:

1. Постройте уравнение множественной регрессии и поясните эко­номический смысл его параметров.

2. Определите частные коэффициенты эластичности и стандартизо­ванные коэффициенты регрессии.

3. Найдите частные и множественный коэффициенты корреляции.

4. Оцените значимость уравнения регрессии с помощью F-критерия Фишера.

Задача 50.По 25 территориям страны изучается влияние климатических ус­ловий на урожайность зерновых у (ц/га). Для этого были отобраны две объясняющие переменные: х1 - количество осадков в период вегетации (мм); х2 - средняя температура воздуха (С). Матрица парных коэффициентов корреляции этих показателей имеет следующий вид:

    у х1 х2
У x1 х2 1,0 0,6 -0,5   1,0 -0,9     1,0

Задание:

1. Определите частные коэффициенты корреляции результата с каж­дым из факторов. Прокомментируйте различие полученных парных и частных коэффициентов корреляции результатов.

2. Исследователь, анализирующий данную зависимость, намерен определить на основе приведенной выше матрицы, какое уравнение регрессии лучше строить:

а) парную линейную регрессию у на х1;

б) парную линейную регрессию у на х2;

в) множественную линейную регрессию.

3. Постройте уравнение регрессии в стандартизованном масштабе и сделайте выводы.

Задача 51.По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей:

    У X1 Х2 Х3
у X1 Х2 Х3 1,00 0,30 0,60 0,40   1,00 0,10 0,15     1,00 0,80   1,00

Задание:

1. Постройте уравнение регрессии в стандартизованном виде и сде­лайте выводы.

2. Определите показатель множественной корреляции (нескорректи­рованный и скорректированный).

3. Оцените целесообразность включения переменной х1 в модель после введения в нее переменных х2 и х3.

Задача 52. Существует закономерность, согласно которой младенцы мужского пола имеют в среднем больший вес при рождении по сравнению с младенцами жен­ского пола. Определяя фиктивную переменную М = 1 для мальчиков и М = 0 для девочек и используя выборку из 964 родов, получим следующую оценку ре­грессионной зависимости веса новорожденного от показателя курения и фик­тивной переменной М:

y=3354+119M-7,0x; R2 = 0,033.

(20) (26) (2,1) В скобках указаны стандартные ошибки.

Задание: Дайте полную интерпретацию регрессии и выполните соответствующие стати­стические проверки.

Задача 53. Изучается зависимость спроса на персональные компьютеры - у от дохода на одного члена семьи - х. Результаты опроса мужчин и женщин представлены на рис.1а, а результаты опроса всех взрослых в зависимости от жилищных условий приведены на рис. 1б.

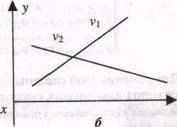
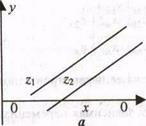
Рис. 1а и 1б. Зависимость спроса на ПК -у (тыс. руб.) от дохода на одного члена семьи -х (тыс. руб.) по данным опроса: а - мужчин (z1) и женщин (z2), б - всего населения при разных жилищных условиях (V1 - хорошие,V2 - плохие)

Задание:

1. Определите, в каком случае возможно построение уравнения рег­рессии с включением фиктивной переменной.

2. Напишите общий вид уравнения регрессии с фиктивной перемен­ной.

3. Укажите, как можно ввести в модель фиктивную переменную и как интерпретировать коэффициент регрессии при ней.

Задача 54. Построена регрессионная модель на основании поквартальных данных о жилищном строительстве за 1996-2001 гг. (в млн.рублей). Оценка регрессионной зависимости этого показателя от временного тренда и сезонных фиктивных и переменных, определенных для II, III и IV кварталов, дала следующий результат (в скобках указаны стандартные ошибки):

у= 13,59 + 3,03S2 + 4,07S3 + 2,99S4 - 0,32t; R2 =0,84

(0,65) (0,74) (0,72) (0,73) (0,04)

Задание:

1.Дайте полную интерпретацию регрессионной модели и оцените значимость каждого фактора.

2.Почему в модель не была включена четвертая переменная, характеризующая 1 квартал?

Задача 55. Администрация банка изучает динамику депозитов физических лиц за ряд лет (млн долл. в сопоставимых ценах). Исходные данные представлены ниже:

Время, лет
Депозиты физических лиц, х

Известно также следующие Sх2=511

Задание:

1. Постройте уравнение линейного тренда и дайте интерпретацию его параметров.

2. Определите коэффициент детерминации для линейного тренда.

3. Администрация банка предполагает, что среднегодовой абсо­лютный прирост депозитов физических лиц составляет не менее 2,5 млн. долл. Подтверждается ли это предположение результатами, которые вы получили?

Задача 56.Управление сельского хозяйства изучает динамику численности тракторов и комбайнов, имеющихся в хозяйствах района за ряд лет (тыс. единиц).

Время, лет
Численность тракторов и комбайнов, тыс. ед.

Известно также следующие Sх2=511

Задание:

1. Постройте уравнение линейного тренда и дайте интерпретацию его параметров.

2. Определите коэффициент детерминации для линейного тренда.

3. Работники управления предполагают, что среднегодовой абсо­лютный прирост численности техники составляет не менее 2,5 тыс. единиц. Подтверждается ли это предположение результатами, которые вы получили?

Задача 57.Изучается динамика потребления мяса в регионе. Для этого были собраны данные об объемах среднедушевого потребления мяса уt (кг) за 7 месяцев. Предварительная обработка данных путем лога­рифмирования привела к получению следующих результатов:

Месяц
ln yt 2,10 2,11 2,13 2,17 2,22 2,28 2,31

Задание:

1. Постройте уравнение экспоненциального тренда.

2. Дайте интерпретацию его параметров.

Задача 58.Имеются данные об урожайности зерновых в хозяйстве:

годы
урожайность, ц/га 25,6 22,4 22,8 21,3 19,8 20,4 19,6 17,3 18,4 17,1 15,9 16,1 15,8 14,4 14,7

Задание:

1. Выделите тенденцию в данном динамическом ряду разными способами.

2. Дайте прогноз урожайности зерновых на два следующих года.

Задача 59. Имеются данные об урожайности зерновых в хозяйстве:

годы
урожайность, ц/га 10,2 10,8 11,8 13,0 14,8 17,2 20,1 23,2

Задание:

1. Обоснуйте выбор типа уравнения тренда.

2. Рассчитайте параметры уравнения тренда.

3. Дайте прогноз урожайности зерновых на следующий год.

Задача 60.Имеются данные об уровне безработицы уt (%) за 8 месяцев:

Месяц
yt 8,8 8,6 8,4 8,1 7,9 7,6 7,4 7,0

Задание:

1. Определите коэффициенты автокорреляции уровней этого ряда первого и второго порядка.

2. Обоснуйте выбор уравнения тренда и определите его параметры.

3. Интерпретируйте полученные результаты.

Задача 61.Пусть имеется следующий временной ряд:

t
xt ... ... ...      

Известно также, что Sxt = 150, Sх2t =8100, Sxt xt-1 = 7350 (t=2..n).

Задание:

1. Определите коэффициент автокорреляции уровней этого ряда первого порядка.

2. Установите, включает ли исследуемый временной ряд тенденцию.

Задача 62. На основе данных по приросту мяса КРС за 24 месяца получены следующие значения коэффициентов автокорреляции уровней первого и т.д. порядков:

r1 = 0,71; r2 = 0,83; r3 = 0,91; r4 = 0,51; r5 = 0,68; r6 = 0,38.

Задание:

1. Охарактеризуйте структуру ряда, определив наличие тенденции и циклических колебаний.

2.Обоснуйте выбор уравнения регрессии для прогноза будущих значений ряда.

Задача 63.Имеются поквартальные данные изменения объемов сельскохозяйственного производства (в сопост. ценах % к предыдущему году).

Номер квартала Объем производства, % к предыдущему периоду Номер квартала Объем производства, % к предыдущему периоду
100,0 98,8
93,9 101,9
96,5 113,1
101,8 98,4
107,8 97,3
96,3 102,1
95,7 97,6
98,2 83,7
104,0 84,3
99,0 88,4

Задание:

1. Постройте график временного ряда.

2. Постройте аддитивную и мультипликативную модели временного ряда.

3. Оцените качество каждой модели через показатели средней абсо­лютной ошибки и среднего относительного отклонения. Выберите лучшую модель.

Задача 64.Имеются данные об объеме экспорта зерна из региона (тонн) за 1998-2003 гг.

Номер Квартала Экспорт, тонн   Номер квартала Экспорт, тонн  

Задание:

1. Постройте график временного ряда.

2. Постройте аддитивную и мультипликативную модели временного ряда.

3. Оцените качество каждой модели через показатели средней абсо­лютной ошибки и среднего относительного отклонения. Выберите лучшую модель.

Задача 65.Для прогнозирования объема продаж колбасных изделий (млн.руб.) на основе поквартальных данных за 2000-2004 гг. была построена аддитивная модель временного ряда объема продаж. Уравнение, мо­делирующее динамику трендовой компоненты этой модели, имеет вид: Т= 100 + 2 • t (при построении тренда для моделирования пере­менной времени использовались натуральные числа, начиная с 1). Показатели за 2003 г., полученные в ходе построения аддитивной модели, представлены в таблице.

Время года Фактический объем продаж в 2003 г. Компонента, полученная по аддитивной модели
трендовая сезонная случайная
Зима         +4
Весна         +5
Лето        
Осень                

Задание:Определите недостающие в таблице данные, учитывая, что объ­ем продаж перерабатывающего цеха колбасных изделий за 2003 г. в целом составил 490 млн. руб.

Задача 66.На основе помесячных данных о потреблении электроэнергии в регионе (млн кВт*ч) за последние 3 года была построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за соответствующие месяцы приводятся ниже:

Январь +25 Май -32 Сентябрь +3
Февраль +10 Июнь -39 Октябрь +14
Март +6 Июль -22 Ноябрь +27
Апрель -4 Август -20 Декабрь ?

Уравнение тренда выгладит следующим образом: Т = 300 +1,4t,

(при расчете параметров тренда для моделирования переменной времени использовались натуральны