Задача 2.
Десезонализированный ряд данных представляет собой последовательность значений, отражающих влияние как трендовой, так и случайной составляющих временного ряда. Как уже отмечалось выше, значения трендовой компоненты должны не просто представлять собой возрастающую последовательность чисел, но и подчиняться некоторому правилу, закономерности, отражающей, по мнению исследователя, основную тенденцию изменения средних объемов продаж. Пусть исследователь полагает, что наиболее вероятной тенденцией изменения объемов продаж является их дальнейший рост с постоянным абсолютным приростом. Математически эту предпосылку можно формализовать с помощью линейной зависимости 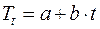 , где
, где 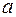 и
и  – произвольные параметры модели, отражающие начальный уровень тренда и величину постоянного прироста соответственно.
– произвольные параметры модели, отражающие начальный уровень тренда и величину постоянного прироста соответственно.
Значения параметров исследователь может задать субъективно, основываясь на своем опыте и интуиции. Однако если этого опыта недостаточно, то оценку параметров можно произвести на основе имеющихся десезонализированных данных, предполагая, что будущие изменения средних объемов продаж тесно связаны с их предыдущими значениями, или, другими словами, предполагая, что искомый линейный тренд имел место и в предыдущие моменты времени.
Итак, требуется подобрать такие значения параметров 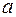 и
и  , чтобы линейный тренд
, чтобы линейный тренд 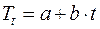 точно отражал растущий средний уровень объемов продаж за последние три года. Возникает вопрос: как? Если найти средние десезонализированные объемы продаж для каждого года, то можно убедиться, что ни при каких значениях параметров эти объемы и соответствующие им моменты времени не удовлетворяют одновременно одной и той же линейной модели. Следовательно, необходимо изменить модель или по другому сформулировать критерий выбора значений параметров. Пойдем по второму пути и выберем в качестве критерия отбора требование минимизировать случайные отклонения десезонализированных данных от линейного тренда.
точно отражал растущий средний уровень объемов продаж за последние три года. Возникает вопрос: как? Если найти средние десезонализированные объемы продаж для каждого года, то можно убедиться, что ни при каких значениях параметров эти объемы и соответствующие им моменты времени не удовлетворяют одновременно одной и той же линейной модели. Следовательно, необходимо изменить модель или по другому сформулировать критерий выбора значений параметров. Пойдем по второму пути и выберем в качестве критерия отбора требование минимизировать случайные отклонения десезонализированных данных от линейного тренда.
Так как согласно аддитивной модели десезонализированные уровни ряда можно представить в виде 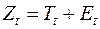 , то необходимо минимизировать выражения
, то необходимо минимизировать выражения 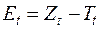 . Поскольку мы заинтересованы в минимально возможных значениях всех случайных отклонений, то необходимо построить и минимизировать критерий, включающий в себя все эти разности. Первая мысль, которая, как правило, приходит на ум, – это найти сумму всех случайных отклонений. Недостаток этой идеи заключается лишь в том, что случайные отклонения часто имеют разные знаки, поэтому сумма отклонений
. Поскольку мы заинтересованы в минимально возможных значениях всех случайных отклонений, то необходимо построить и минимизировать критерий, включающий в себя все эти разности. Первая мысль, которая, как правило, приходит на ум, – это найти сумму всех случайных отклонений. Недостаток этой идеи заключается лишь в том, что случайные отклонения часто имеют разные знаки, поэтому сумма отклонений  и
и 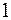 будет равносильна сумме отклонений
будет равносильна сумме отклонений 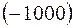 и
и  , что с экономической точки зрения, конечно, не так.
, что с экономической точки зрения, конечно, не так.
Устранить влияние знака можно, взяв каждое случайное отклонение по модулю. В этом случае необходимо будет найти такие значения параметров 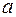 и
и  , при которых функция
, при которых функция 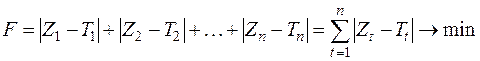 . Такой способ оценки параметров называется методом наименьших модулей. Этот метод не получил широкого распространения из-за своей неоднозначности (одно и то же минимальное значение суммы может достигаться при различных значениях параметров) и трудоемкости вычислительной процедуры.
. Такой способ оценки параметров называется методом наименьших модулей. Этот метод не получил широкого распространения из-за своей неоднозначности (одно и то же минимальное значение суммы может достигаться при различных значениях параметров) и трудоемкости вычислительной процедуры.
Другой способ устранить влияние знака заключается в возведении каждого случайного отклонения в квадрат, т.е. в минимизации функции
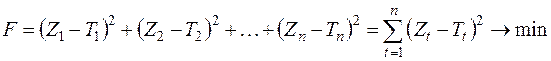 .
.
Этот способ называется методом наименьших квадратов. Его отличают единственность решения, относительно простая вычислительная процедура, хорошие статистические свойства получаемых оценок, поэтому он до сих пор является наиболее распространенным методом оценки параметров моделей.
Итак, применяя метод наименьших квадратов, найдем параметры линейного тренда 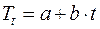 , т.е. найдем значения параметров
, т.е. найдем значения параметров 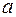 и
и  , которые минимизируют значение функции
, которые минимизируют значение функции  . Необходимым условием экстремума функции двух переменных является равенство нулю соответствующих частных производных, которые в данном случае определены в любой точке двумерного пространства. Найдя эти частные производные и приравняв их нулю, после несложных преобразований получаем следующую систему из двух уравнений с двумя неизвестными:
. Необходимым условием экстремума функции двух переменных является равенство нулю соответствующих частных производных, которые в данном случае определены в любой точке двумерного пространства. Найдя эти частные производные и приравняв их нулю, после несложных преобразований получаем следующую систему из двух уравнений с двумя неизвестными:
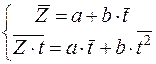 (1)
(1)
Решая эту систему в общем виде, получаем формулы для оценки параметров линейного тренда с помощью метода наименьших квадратов:
return false">ссылка скрыта ,
, 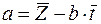 (2)
(2)
Используя десезонализированные значения из таблицы 5, рассчитаем все необходимые средние значения в таблице 6, при необходимости округляя получаемые значения до сотых.
Расчет средних значений для оценки параметров линейного тренда. Таблица 6
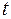
| 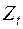
| 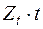
| 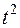
| |
| 962,5 | 962,5 | |||
| 1247,5 | ||||
| 1182,5 | 3547,5 | |||
| 1147,5 | ||||
| 1442,5 | 7212,5 | |||
| 1687,5 | ||||
| Сумма | 28932,5 | |||
| Среднее | 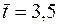
| 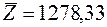
| 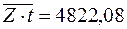
| 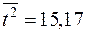
|
Подставляя полученные значения средних в формулы (2), имеем:
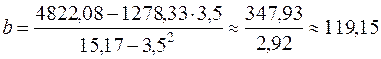 ,
,
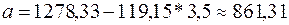 .
.
Отсюда, 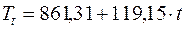 .
.
Таким образом, используя значения сезонных колебаний, рассчитанные в задаче 1, 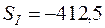 ,
, 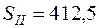 , на основе аддитивной модели найдем прогнозные значения объемов продаж на следующие два полугодия:
, на основе аддитивной модели найдем прогнозные значения объемов продаж на следующие два полугодия:
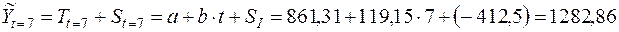
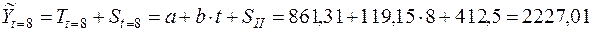 (3)
(3)
(обозначения  указывают на то, что прогнозные значения объемов продаж рассчитаны без учета случайной компоненты временного ряда, точные значения которой неизвестны по определению).
указывают на то, что прогнозные значения объемов продаж рассчитаны без учета случайной компоненты временного ряда, точные значения которой неизвестны по определению).
Итак, опираясь на предпосылку о стабильном росте объемов продаж с постоянным абсолютным приростом и постоянными сезонными колебаниями, можно предположить, что объемы продаж зимней одежды в магазинах рассматриваемой сети составят в первом полугодии 2009г. 1282,86 тыс. руб., а во втором – 2227,01 тыс.руб.