Построение гиперболической функции
Уравнение гиперболической функции : ŷ = a + b / x .
Произведем линеаризацию модели путем замены Х = 1 / х. В результате получим линейное уравнение
ŷ = a + b Х.
Рассчитаем его параметры по данным таблицы 3.8
Таблица 3.8.
| t |
|
|
|

|

|

|  
|

|

|
| 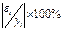
| |
| 0,0156 | 1,0000 | 0,0002441 | 13,43 | 180,33 | 61,5 | 2,489 | 6,1954 | 3,889 | ||||
| 0,0147 | 0,8235 | 0,0002163 | 5,43 | 29,47 | 58,2 | -2,228 | 4,9637 | 3,978 | ||||
| 0,0122 | 0,6341 | 0,0001487 | 1,43 | 2,04 | 49,3 | 2,740 | 7,5089 | 5,270 | ||||
| 0,0132 | 0,6316 | 0,0001731 | -2,57 | 6,61 | 52,7 | -4,699 | 22,078 | 9,789 | ||||
| 0,0119 | 0,5952 | 0,0001417 | -0,57 | 0.32653 | 48,2 | 1,777 | 3,1591 | 3,555 | ||||
| 0,0104 | 0,4792 | 0,0001085 | -4,57 | 20,90 | 42,9 | 3,093 | 9,5648 | 6,723 | ||||
| 0,0100 | 0,3800 | 0,0001000 | -12,57 | 158,04 | 41,4 | -3,419 | 11,69 | 8,997 | ||||
| итого | 0,0880 | 4,5437 | 0,0011325 | 397,71 | 354,2 | -0,246 | 65,159 | 42,202 | ||||
| ср знач | 50,57 | 0,0126 | 0,6491 | 0,0001618 | 6,029 | |||||||

Получим следующее уравнение гиперболической модели:
ŷ=5,7 + 3571,9 / х
Определим индекс корреляции

Связь между показателем y и фактором x можно считать достаточно сильной.
Индекс детерминации:
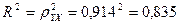
Вариация результата Y (объема выпуска продукции) на 83,5 % объясняется вариацией фактора Х (объемом капиталовложений).
F-критерий Фишера:

F>FТАБЛ = 6,61 для a = 0,05 ; к1=m=1, k2=n-m-1=5 .
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ .
Средняя относительная ошибка
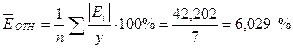
В среднем расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 6,029 %.
Для выбора лучшей модели построим сводную таблицу результатов.
Таблица 3.9.
 Параметры
Модель Параметры
Модель
| Коэффициент детерминации R2 | F-критерий Фишера | Индекс корреляции ryx (ryx) | Средняя относительная ошибка Еотн |
| 1.Линейная | 0,822 | 23,09 | 0,907 | 5,685 |
| 2.Степенная | 0,828 | 24,06 | 0,910 | 6,054 |
| 3.Показательная | 0,828 | 24,06 | 0,910 | 5,909 |
| 4.Гиперболическая | 0,835 | 25,30 | 0,914 | 6,029 |
Все модели имеют примерно одинаковые характеристики, но большее значение F – критерия Фишера и большее значение коэффициента детерминации R2 имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.
Расчет прогнозного значения результативного показателя:
Прогнозное значение результативного признака (объема выпуска продукции) определим по уравнению гиперболической модели, подставив в него планируемую (заданную по условию) величину объема капиталовложений :
ŷПР = 5,7 + 3571,9/ ХПР = 5,7 + 3571,9/ 89,573 = 45,542 (млн. руб.)
Вариант 1
| ||||||||||

|
Вариант 2
| ||||||||||

|
Вариант 3
| ||||||||||

|
Вариант 4
| ||||||||||

|
Вариант 5
| ||||||||||

|
Вариант 6
| ||||||||||

|
Вариант 7
| ||||||||||

|
Вариант 8
| ||||||||||

|
Вариант 9
| ||||||||||

|
Вариант 10
| ||||||||||

|
Вариант 11
| ||||||||||

|
Вариант 12
| ||||||||||

|
Вариант 13
| ||||||||||

|
Вариант 14
| ||||||||||

|
Вариант 15
| ||||||||||

|
Вариант 16
| ||||||||||

|
Вариант 17
| ||||||||||

|
Вариант 18
| ||||||||||

|
Вариант 19
| ||||||||||

|
Вариант 20
| ||||||||||

|
Приложения
Приложение 1. Значения F-критерия Фишера при уровне значимости a=0,05.
| Число степеней свободы знаменателя (k2) | Число степеней свободы числителя (k1) | |||||||||
| ¥ | ||||||||||
| 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 | |
| 18,5 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3.63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2.22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,52 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1.74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| '3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79. | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
| ¥ | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
return false">ссылка скрыта
Приложение 2. Значения t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01 (двухсторонний)
| Число степеней свободы k | a | Число степеней свободы k | a | ||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | ||
| 6,3138 | 12,706 | 63,657 | 1,7341 | 2,1009 | 2,8784 | ||
| 2,9200 | 4,3027 | 9,9248 | 1,7291 | 2,0930 | 2,8609 | ||
| 2,3534 | 3,1825 | 5,8409 | 1,7247 | 2,0860 | 2,8453 | ||
| 2,1318 | 2,7764 | 4,6041 | 1,7207 | 2,0796 | 2,8314 | ||
| 2,0150 | 2,5706 | 4,0321 | 1,7171 | 2,0739 | 2,8188 | ||
| 1,9432 | 2,4469 | 3,7074 | 1,7139 | 2,0687 | 2,8073 | ||
| 1,8946 | 2,3646 | 3,4995 | 1,7109 | 2,0639 | 2,7969 | ||
| 1,8595 | 2,3060 | 3,3554 | 1,7081 | 2,0595 | 2,7874 | ||
| 1,8331 | 2,2622 | 3,2498 | 1,7056 | 2,0555 | 2,7787 | ||
| 1,8125 | 2,2281 | 3,1693 | 1,7033 | 2,0518 | 2,7707 | ||
| 1,7959 | 2,2010 | 3,1058 | 1,7011 | 2,0484 | 2,7633 | ||
| 1,7823 | 2,1788 | 3,0545 | 1,6991 | 2,0452 | 2,7564 | ||
| 1,7709 | 2,1604 | 3,0123 | 1,6973 | 2,0423 | 2,7500 | ||
| 1,7613 | 2,1448 | 2,9768 | 1,6839 | 2,0211 | 2,7045 | ||
| 1,7530 | 2,1315 | 2,9467 | 1,6707 | 2,0003 | 2,6603 | ||
| 1,7459 | 2,1199, | 2,9208 | 1,6577 | 1,9799 | 2,6174 | ||
| 1,7396 | 2,1098 | 2,8982 | ¥ | 1,6449 | 1,9600 | 2,5758 |
Приложение 3. Критические границы отношения R/S
| п | Нижние границы | Верхние границы | ||
| а = 0,05 | а =0,10 | а =0,10 | а = 0,05 | |
| 2,50 | 2,59 | 3,308 | 3,399 | |
| 2,67 | 2,76 | 3,57 | 3,685 | |
| 2,80 | 2,90 | 3,78 | 3,91 | |
| 2,92 | 3,02 | 3,95 | 4,09 | |
| 3,01 | 3,12 | 4,09 | 4,24 | |
| 3,10 | 3,21 | 4,21 | 4,37 | |
| 3,18 | 3,29 | 4,32 | 4,49 | |
| 3,34 | 3,45 | 4,53 | 4,71 | |
| 3,47 | 3,59 | 4,70 | 4,89 | |
| 3,58 | 3,70 | 4,84 | 5,04 | |
| 3,67 | 3,79 | 4,96 | 5,16 | |
| 3,75 | 3,88 | 5,06 | 5,26 | |
| 3,83 | 3,95 | 5,14 | 5,35 |
Приложение 4.d-статистика Дарбина - Уотсона: d1 и d2, уровень значимости в 5%
| n | k =1 | k =2 | ||||||
| d1 | d2 | d1 | d2 | |||||
| 1,08 | 1,36 | 0,95 | 1,54 | |||||
| 1,10 | 1,37 | 0,98 | 1,54 | |||||
| 1,13 | 1,38 | 1,02 | 1,54 | |||||
| 1,16 1,16 | 1,39 | 1,05 | 1,53 | |||||
| 1,18 | 1,40 | 1,08 | 1,53 | |||||
| I,20 | 1,41 | 1,10 | 1,54 | |||||
| 1,22 | 1,42 | 1,13 | 1,54 | |||||
| 1,24 | 1,43 | 1,15 | 1,54 | |||||
| 1,26 | 1,44 | 1,17 | 1,54 | |||||
| 1,27 | 1,45 | 1,19 | 1,55 | |||||
| 1,29 | 1,45 | 1,21 | 1,55 | |||||
Литература