Построение линейной модели парной регрессии

Определим линейный коэффициент парной корреляции по следующей формуле:

 

;

 

Можно сказать, что связь между объемом капиталовложений Х и объемом выпуска продукции Y обратная, достаточно сильная.

Уравнение линейной регрессии имеет вид: ŷ = a + b ´ x

 

Таблица 3.5

t	y	x	y´x	x´x				2
					13.43	180.36	-17.4	303.8	60.2	3.84	6.000
					5.43	29.485	-13.4	180.36		-1.96	-3.500
					1.43	2.0449	0.57	0.3249	50.3	1.74	3.346
					-2.57	6.6049	-5.43	29.485	53.6	-5.56	-11.583
					-0.57	0.3249	2.57	6.6049	49.2	0.84	1.680
					-4.57	20.885	14.57	212.28	42.6	3.44	7.478
					-12.6		18.57	344.84	40.4	-2.36	-6.211
итого					0.01	397.71		1077.7		-0.02	39.798
ср.знач	50.57	81.43	4033.14	6784.57							5.685
диспер	56.8

 

Значения параметров a и b линейной модели определим, используя данные таблицы 3.5

 

 

Уравнение линейной регрессии имеет вид:

ŷ = 95,36 - 0,55 ´ х

С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.

Рассчитаем коэффициент детерминации:

R² = r²_yx = 0,822

Вариация результата Y (объема выпуска продукции) на 82,2 % объясняется вариацией фактора Х (объемом капиталовложений).

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

F>F_ТАБЛ = 6,61 для a = 0,05 ; к1=m=1, k2=n-m-1=5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>F_ТАБЛ .

Определим среднюю относительную ошибку:

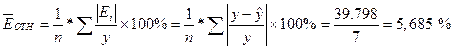
В среднем расчетные значения ŷ для линейной модели отличаются от фактических значений на 5,685 %.