Шар, тор и кольцо

 

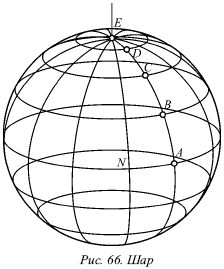
Когда некоторая ось вращения I является диаметром окружности, то получается шаровая поверхность (рис. 66).

 

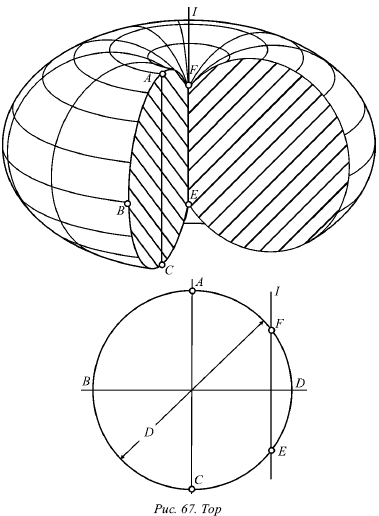
Если положение оси другое, в плоскости окружности получается поверхность, называемая тором (рис. 67).

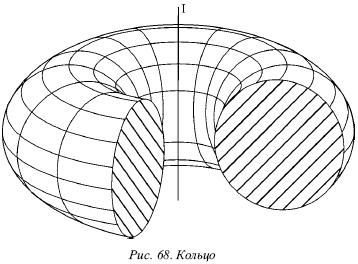
Когда ось вращения не пересекает окружность (рис. 68), то полученную в этом случае поверхность обычно называются кольцом (или кольцевой поверхностью).

Рассмотрим эти поверхности отдельно.

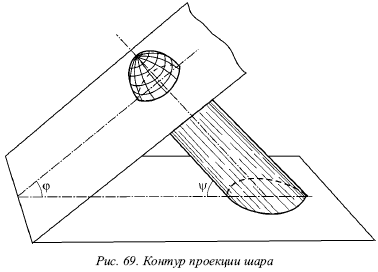
Для того чтобы построить контур проекции шара, необходимо провести все проецирующие лучи, которые касаются ее поверхности (рис. 69). Эти лучи образуют цилиндр, касающийся шара по большому кругу, плоскость которого Q перпендикулярна проецирующим лучам.

В случае, если плоскость проекции перпендикулярна лучам проекции, проекцией шара будет окружность, которая равна большому кругу шара. В других случаях проекция будет иметь форму эллипса.

Итак, прямоугольная проекция шара – круг, косоугольная проекция – эллипс.

Следовательно, проекции контура шара на горизонтальных, фронтальных и профильных плоскостях всегда являются окружностью.

 

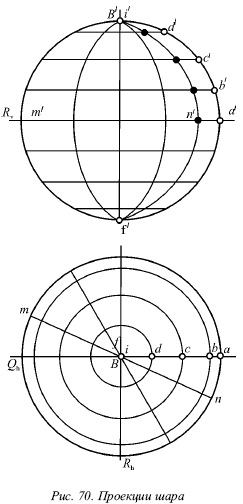
Шаровую поверхность можно получить вращением окружности около ее диаметра. Пусть ось вращения I является перпендикулярной горизонтальной плоскости и становится одним из диаметров окружности. Окружность будет вращаться около оси I и описывать шаровую поверхность (рис. 66). Точки, которые лежат на этой исходной окружности (А, В, С и D), при вращении ее вокруг оси I также опишут окружности, называемые параллелями. Параллели изображаются без искажения на горизонтальной плоскости, а на фронтальной плоскости – в виде отрезков, равных диаметрам (рис. 70).

 

Самая большая параллель равна большому кругу шара. Она называется его экватором. Проекции экватора показаны на рисунке 70 штриховой линией.

Разные положения вращающейся вокруг оси I окружности выступают как так называемые меридианы шара. Их изображают на горизонтальной плоскости в форме диаметров окружности, которые представляют собой контуры проекции шара. На фронтальной плоскости все меридианы, кроме двух, изображаются в виде эллипсов. Меридиан, находящийся во фронтальной плоскости, будет изображаться в виде контура на этой проекции и в виде вертикального диаметра на остальных проекциях. Подобным образом изображается меридиан, который расположен в профильной плоскости.

 

Точки пересечения поверхности шара с осью вращения (Е и F, рис. 65) принято называть полюсами.

 

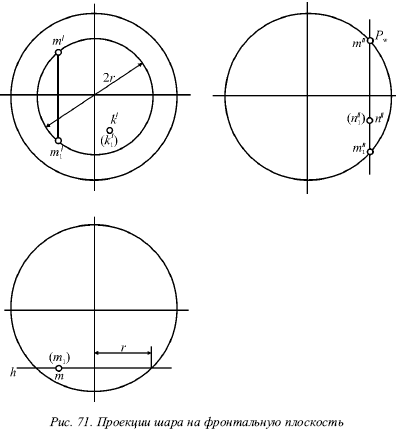
Любое из сечений шара плоскостью будет являться окружностью. Она проецируется на данную плоскость проекций без искажения только тогда, когда секущая плоскость параллельна рассматриваемой плоскости горизонтальной проекции. На рисунке 71 показана фронтальная плоскость. Окружность, по которой эта плоскость пересекает поверхность шара, проецируется на фронтальную плоскость без искажения. На горизонтальной и профильной плоскостях эта окружность проектируется в форме отрезков, которые совпадают со следами P_h и P_w и двумя точками контуров горизонтальной и профильной проекций шара, заключенных между ними. Длины отрезков равны диаметру полученной окружности.

 

На рисунке 70 показаны семь горизонтальных плоскостей, которые пересекают шар по горизонтально расположенным окружностям. Данные окружности проецируются на горизонтальную плоскость в полную величину, а на фронтальную плоскость – в виде отрезков. Одна плоскость проходит через центр шара и делит его на две равные части. Верхняя половина шара является видимой при наблюдении сверху, а точки, находящиеся на нижней, невидимы.

 

Также проведены шесть окружностей, представляющих собой различные положения вращающейся вокруг оси I окружности; одна из них является сечением шара фронтальной плоскостью. Эта фронтальная плоскость разделяет шар на две половины. Его передняя часть видна на фронтальной проекции. Еще одна окружность получена в результате сечения профильной плоскостью. Она также отделяет видимые точки шара от невидимых на профильной проекции. Остальные четыре окружности являются сечениями шара горизонтально‑проецирующими плоскостями. Все эти четыре окружности имеют горизонтальные проекции в виде отрезков, равных диаметру шара, а фронтальные проекции – в виде эллипсов.

Тор – это поверхность, получаемая в результате вращения окружности около оси, которая лежит в ее плоскости, не проходящей через ее центр.

На рисунке 67 показаны окружность и ось вращения I, пересекающая окружность в двух точках (F и Е).

Если вращать большую часть FABCE окружности, то получается тор, показанный на рисунке 67.

Если вращать меньшую дугу РВЕ окружности, то получается поверхность тора, которая напоминает по форме лимон (рис. 72).

 

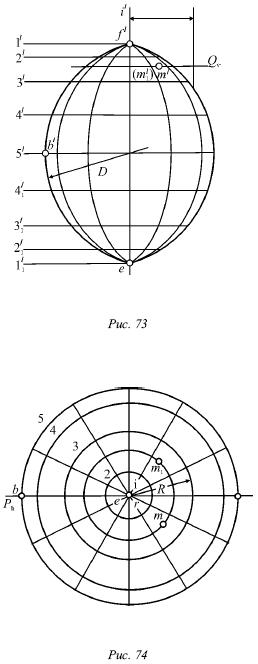
Дуга полуокружности ABC (рис. 74) образует при вращении ту часть поверхности тора, которую принято называть наружной, а две небольшие дуги AF и СЕ – внутренней его поверхность.

 

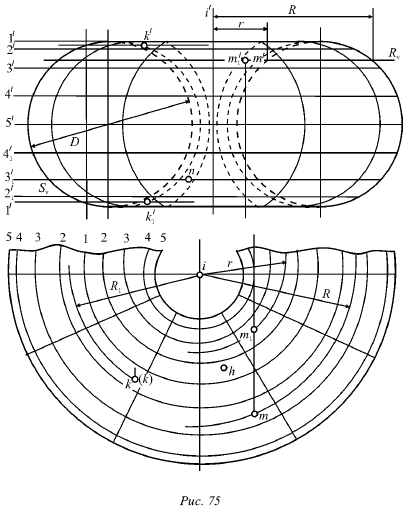
Точка В при вращении описывает самую большую окружность (ее можно назвать экватором тора). Эта окружность отделяет видимую часть поверхности тора от невидимой, если смотреть на тор сверху. Дуги окружности BAF или BF (рис. 75) описывают при вращении видимые части поверхности, а дуги ВСЕ или BE – невидимые.

При наблюдении тора спереди вся его внутренняя поверхность будет невидимой. Если провести фронтальную плоскость через ось вращения I, то эта плоскость разделит наружную поверхность тора на переднюю видимую и заднюю невидимую.

Рассмотрим образования кольца. В этом случае ось вращения I, несмотря на то что лежит в плоскости исходной окружности, ее не пересекает (рис. 73). Любая горизонтальная плоскость, перпендикулярная оси вращения, даст в сечении две окружности. На рисунке 74 проведена плоскость R, пересекающая кольцевую поверхность по двум окружностям (с радиусаи R и r), т. е. по двум параллелям.