Вероятностные характеристики случайных переменных
Определение функции плотности вероятности 
– Функция, которая для любого интервала [x1, x2] на 0х позволяет определить вероятность того, что случайная переменная х находится в этом интервале.
Р(х1 
х2)= 
Матожидание случайной величины - средневзвешенного значение данной случайной величины:
Для Д. с/в – М (х) (в зап.уч.- Е (х) ):
М(х)= 
Для Н. с/в:
М (х)= 
- не собственный интеграл.
Свойства:
1. М(const)= const
2. M(aX+b)=aM(X)+b, a,b- const;
3. M(X+Y)= M(X)+M(Y), X,Y- независимые случайные переменные;
4. M(X*Y) = M(X)*M(Y), X,Y- независимые случайные переменные.
Дисперсия - отражает относительно, разброса случайной величины относительно среднего значения (рассеяние около среднего значения)
Для Д. с/в:
Д(х)= (х – М(х))2=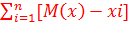 
2pi;
Для Н. свойств:
Д(х)= 
2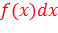 
Свойства Д (Х):
1. Д (а)=0;
2. Д (Х+У) =Д (Х)+Д (У);
3. Д (аХ) =а2Д (Х)
4. Д(Х) = М(Х2) – [М(Х)]2
Момент первого порядка есть среднее значение (математическое ожидание) случайной величины Момент второго порядка есть средний квадрат случайной величины.
Часто используется так называемое среднеквадратичное значение случайной величины, представляющее собой корень квадратный из среднего квадрата случайной величины:
Иногда рассматривается центрированное значение случайной величины x0=х-х~, где х~ —среднее значение.
Если х — случайная величина, а х~ — среднее значение этой величины, то величина х-х~ есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величина х.
Средним отклонением А называется среднее значение (математическое ожидание) абсолютной величины отклонения.
Среднее отклонение случайной величины является уже не случайной величиной, а обычным числом.
Укажем простейшие свойства среднеквадратичных отклонений.
1. При сложении независимых случайных величин дисперсии складываются:
Поэтому среднеквадратичное отклонение суммы независимых случайных величин
Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок.
2. Пусть имеется п случайных величин с одинаковыми средними значениями а; и с одинаковыми законами распределения. Тогда их среднее арифметическое тоже будет случайной величиной с тем же самым средним значением но среднеквадратичное отклонение его будет в раз меньше, чем для каждой из составляющих (в случае независимых случайных величин):
Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое, хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквадратичное отклонение), чем каждое измерение в отдельности. Здесь случайные ошибки измерения в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой массовостью измерений скомпенсированы быть не могут.
3. Для п случайных величин, независимых и имеющих одно и то же среднее значение х~, среднее арифметическое будет при достаточно большом п как угодно мало отличаться от среднего значения х~ (с вероятностью, как угодно близкой к единице). Замечание в скобках означает, что это практически достоверно, но не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом п и указанных условиях
Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет первостепенное значение для обработки экспериментальных данных и для учетной статистики.
Введем теперь понятие интегрального закона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, меньшее некоторого значения х.
0.3.2.Законы распределения:
1. Нормальное распределение:
а - математическое ожидание
2. распределение Стьюдента (t-распределение с n - степенями свободы)
Пусть x и x2 – независимые сложные переменные, причем х имеет нормальное распределение, а х2-х2 распределение с n - степенями свободы. Тогда
3. распределение Фишера (F-распред.)
Пусть x12 и x22– независимые сложные величины, имеющие x2 – распределение со степенями свободы n1 и n2 соответственно. Тогда
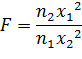
4.равномерное распределение
5 . х2 - распределение с n степенями свободы. Пусть х - независимая сложная переменная, тогда
