N-мерные пространства.
n-мерным пространством мы будем называть пространство точек 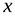 , каждая из которых задается n координатами:
, каждая из которых задается n координатами:  . Расстояние между точками
. Расстояние между точками 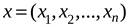 и
и  в таком пространстве определяется следующим образом:
в таком пространстве определяется следующим образом:  . В частности, формула для расстояния между точками используется при сравнении объектов с идеалом по n признакам.
. В частности, формула для расстояния между точками используется при сравнении объектов с идеалом по n признакам.
Линейные отображения.
Линейным отображением 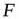 векторного пространства
векторного пространства 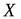 в векторное пространство
в векторное пространство 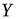 называется такое отображение, что для любых двух векторов
называется такое отображение, что для любых двух векторов 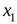 и
и 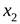 из пространства
из пространства 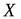 и любых двух вещественных чисел
и любых двух вещественных чисел 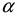 и
и 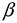 справедливо:
справедливо:
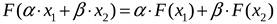 .
.
Любое линейное отображение  -мерного пространства в
-мерного пространства в 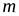 -мерное задается некоторой матрицей размера
-мерное задается некоторой матрицей размера 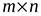 и наоборот, любая матрица размера
и наоборот, любая матрица размера 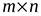 задает линейное отображение
задает линейное отображение  -мерного пространства в
-мерного пространства в 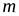 -мерное.
-мерное.
Действительно, возьмем произвольную матрицу  размера
размера 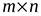 .Ее можно умножить на
.Ее можно умножить на  -мерный вектор
-мерный вектор  , рассматриваемый в вида матрицы-столбца размером
, рассматриваемый в вида матрицы-столбца размером  . Результатом умножения будет матрица-столбец размером
. Результатом умножения будет матрица-столбец размером  , то есть,
, то есть, 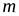 -мерный вектор
-мерный вектор  . Имеем
. Имеем  , где
, где
 ,
,  ,
,  .
.
То, что отображение, задаваемое умножением вектора на матрицу, является линейным, следует из свойств сумм и произведений матриц.
В частности, линейное отображение  -мерного пространства на множество вещественных чисел (одномерное пространство) задается матрицей-строкой размера
-мерного пространства на множество вещественных чисел (одномерное пространство) задается матрицей-строкой размера  .
.