Любая плоскость в пространстве XYZ представляется линейным уравнением вида . И наоборот, любое линейное уравнение задает плоскость.

Взаимное расположение двух плоскостей.Две плоскости, представленные уравнениями 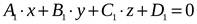и могут 1) совпадать, 2) быть параллельными, 3) пересекаться.

В случае 1) коэффициенты в уравнениях плоскостей могут отличаться только сомножителем, на который можно сократить. Это означает, что должно выполняться соотношение .

В случае 2) нормальные векторы обеих плоскостей должны совпадать, или быть параллельными, но уравнения должны оставаться различными за счет свободных членов. Следовательно, должно выполняться соотношение .

В случае 3) нормальные векторы плоскостей не должны быть параллельными.

Геометрическим местом точек пересечения плоскостей является прямая.

Взаимное расположение трех плоскостей.Вариантов взаимного расположения трех плоскостей значительно больше, чем двух. Мы рассмотрим случаи, когда любые две плоскости из трех не являются ни параллельными, ни, тем более, совпадающими. Это значит, что каждые две плоскости пересекаются вдоль прямой. Выберем какие-то две плоскости и рассмотрим случаи, когда 1) их общая прямая не пересекается с третьей плоскостью, 2) у трех плоскостей общая прямая пересечения, 3) их общая прямая пересекается с третьей плоскостью.

В случае 1) все три прямые, получаемые попарным пересечением плоскостей, параллельны.

Это значит, что все три вектора нормалей к плоскостям можно расположить в одной плоскости, перпендикулярной к трем параллельным прямым. В этом случае , так как один из векторов нормалей является линейной комбинацией двух других.

В случае 2) все три вектора нормалей также можно расположить в одной плоскости – и тот же определитель из коэффициентов равен нулю.

В случае 3) , и общая прямая двух плоскостей пересекает третью плоскость в единственной точке.

Найдемточку пересечения трех плоскостей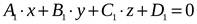, 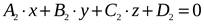и–это значит, найти решение системы

В соответствии с изложенным единственное решение системы возможно только в случае отличия от нуля главного определителя системы: .