Перестановки с повторениями и полиномиальная формула.

Разбиение n- множества на попарно непересекающиеся классы с известным набором чисел элементов классов называется разбиением на блоки длины , где 1£n₁, …, n_k£n, а n₁+…+n_k=n.

Теорема 1. Пусть – число разбиений n-множества длины . Тогда .

Доказательство. Пусть множество 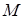разбито на блоки M₁,…,M_k, такие, что |M₁|=n₁,…,|M_k|=n_k, 1£n₁,…,n_k£n, n₁+…+n_k=n.

Элемент множества M₁ можно выбрать способами, элемент множества M₂ – способами, элемент множества M₃ – способами и т.д. Применим правило произведения:

После сокращений получим: .

Докажем теорему о полиномиальной формуле.

Теорема 2. .

Доказательство. После раскрытия степени, подсчитываем число одночленов вида . Их столько же, сколько будет разбиений множества множителей степени на подмножества, содержащие соответственно и имеющие мощность . Потому коэффициент при одночлене равен .

Формула, доказываемая в теореме 2, называется полиномиальной (или формулой полинома Ньютона).

Перестановкой с повторениями называется размещение с повторениями по n из n элементов k-множества M (k£n) со следующим дополнительным условием: различные k элементов множества M повторяются соответственно n₁,…,n_k раз, 1£n₁,…,n_k£n, n₁+…+n_k=n.

Теорема 3. Число перестановок с повторениями различных k элементов n₁,…,n_k раз, 1£n₁,…,n_k£n, n₁+…+n_k=n, равно .

Доказательство. Пусть M – множество номеров перестановки с повторениями, одной из указанных в условии теоремы, M₁,…,M_k – множества номеров с одинаковыми элементами, повторяющимися n₁,…,n_k раз соответственно. Тогда семейство множеств {M₁,…,M_k} будет разбиением множества M на k блоков. Значит, каждой перестановке с повторениями соответствует вполне определенное разбиение множества M на k блоков. Ясно, что это соответствие является биекцией. Значит, искомое число перестановок с повторениями равно числу разбиений на k блоков .