Отношение включения над множествами и его свойства.

Множество 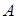называется подмножеством множества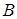 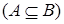, если

.

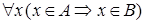Множество 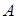называется собственным подмножеством множества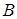 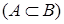, если 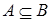и .

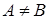Перечислим 4 основные свойства отношения включения между множествами:

1) включение рефлексивно: 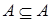для всех множеств ;

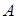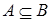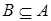2) включение антисимметрично: из и следует ;

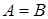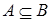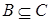3) включение транзитивно: из и следует ;

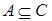4) включение не связно: неверно, что (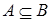или ).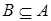

Существует множество, содержащее все подмножества данного множества 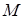. Оно называется множеством всех подмножеств множества 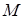и обозначается :

.

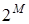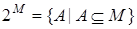Примеры. Если 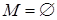, то 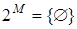. Если 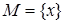, то .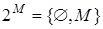

Теорема. Пусть множество 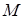конечно. Тогда .

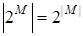Доказательство. Применим математическую индукцию по числу 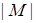элементов множества 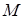. Заметим, что .

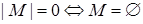База индукции: 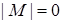. Тогда 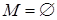, и .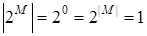

Шаг индукции: допустим, что , и для всех множеств с элементами утверждение теоремы 1 выполнено. Так как 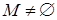, можно выбрать некоторый элемент 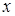множества 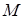. Поскольку 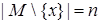, то по индуктивному предположению множество 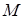имеет 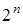подмножеств, не содержащих элемента 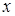. Столько же у него подмножеств, содержащих элемент 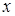. Следовательно, 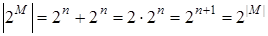. Теорема доказана.