Статистические методы изучения взаимосвязей.
Виды и формы зависимости между социально-экономическими явлениями.
Многообразие взаимосвязей в которых находятся социально-экономические явления, рождают необходимость в их классификации.
По видам различают функциональную и корреляционную зависимость.
Функциональной называют такую зависимость, при которой одному значению факторного признака X соответствует одно строго определенное значение результативного признака Y.
В отличие от функциональной зависимости, корреляционная выражает такую связь между социально-экономическими явлениями, при которой одному значению факторного признака X могут соответствовать несколько значений результативного признака Y.
По направлению различают прямую и обратную зависимость.
Прямой называют такую зависимость, при которой значение факторного признака X и результативного признака Y изменяются в одном направлении. Т.о. при увеличении значения X, значения Y в среднем увеличиваются, а при уменьшении X - Y уменьшается.
Обратная зависимость между факторным и результативным признаками, если они изменяются в противоположных направлениях.
Важное место в статистическом изучении взаимосвязей занимают следующие методы:
1. Метод приведения параллельных данных.
2. Метод аналитических группировок.
3. Графический метод.
4. Балансовый метод.
5. Индексный метод.
6. Корреляционно-регрессионный.
1. Сущность метода приведения параллельных данных заключается в следующем:
Исходные данные по признаку X располагаются в порядке возрастания или убывания, а по признаку Y записываются соответствующие им показатели. Путем сопоставления значений X и Y, делается вывод о наличии и направлении зависимости.
3. Сущность графического метода составляет наглядное представление наличия и направления взаимосвязей между признаками. Для этого значение факторного признака X располагается по оси абсцисс, а значение результативного признака по оси ординат. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости. При этом возможны следующие варианты:
а \, б/ (вверх) , в\ (вниз).
Если точки на графике расположены беспорядочно (а), то зависимость между изучаемыми признаками отсутствует.
Если точки на графике концентрируются вокруг прямой (б)/, зависимость между признаками прямая.
Если точки концентрируются вокруг прямой (в)\, то это свидетельствует о наличии обратной зависимости.
На основе метода параллельных данных и графического метода, могут быть рассчитаны показатели, характеризующие степень тесноты корреляционной зависимости.
Наиболее кратным из них является коэффициент знаков Фехнера. Он рассчитывается по формуле:
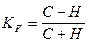
C - сумма совпадающих знаков отклонений индивидуальных значений признака от средней.
H - сумма несовпадений
Данный коэффициент изменяется в пределах (-1;1).
Значение KF=0 свидетельствует об отсутствии зависимости между изучаемыми признаками.
Если KF=±1, то это говорит о наличии функциональной прямой (+) и обратной (-) зависимости. При значении KF>½0,6½ делается вывод о наличии сильной прямой (обратной) зависимости между признаками. Кроме того на основе исходных данных о факторном и результативном признаках, может быть рассчитан коэффициент корреляции рангов Спирмена, который определяется по формуле:

 - квадраты разности рангов
- квадраты разности рангов
(R2-R1), n - число пар рангов
Данный коэффициент, как и предыдущий, изменяется в тех же пределах и имеет одинаковую с KF экономическую интерпретацию.
В тех случаях, когда значение X или Y выражаются одинаковыми показателями, коэффициент корреляции рангов рассчитывается по следующей формуле:

tj - одинаковое число рангов в j - ряду
Если исследуется зависимость между тремя и более математическими признаками, то для ее исследования применяется коэффициент конкордации определяемый по формуле:

m - количество факторов
n - число наблюдений
S - отклонение суммы квадратов рангов от средней квадратов рангов