Нелинейная регрессия. Линеаризация, оценка коэффициентов.
Коэффициент эластичности как характеристика силы связи фактора с результатом.
Корреляция для нелинейной регрессии. Тест Бокса-Кокса.
Нелинейная регрессия. Линеаризация, оценка коэффициентов.
Нелинейная регрессия.
Лекция 3
Вопросы:
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий:
- регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
- регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
- полиномы разных степеней -  ,
,  , … (анализ издержек от объема выпуска);
, … (анализ издержек от объема выпуска);
- равносторонняя гипербола - 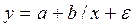 (зависимость между объемом выпуска и средними фиксированными издержками, между доходом и спросом на блага, между уровнем безработицы и процентным изменением заработной платы).
(зависимость между объемом выпуска и средними фиксированными издержками, между доходом и спросом на блага, между уровнем безработицы и процентным изменением заработной платы).
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
- степенная -  (зависимость между расходами и прибылью);
(зависимость между расходами и прибылью);
- показательная -  (производственная функция Кобба-Дугласа);
(производственная функция Кобба-Дугласа);
- экспоненциальная -  (при анализе изменений переменной с постоянным темпом прироста).
(при анализе изменений переменной с постоянным темпом прироста).
Нелинейные регрессии по включаемым переменным позволяют использовать МНК для оценки параметров, так как эти функции линейны по параметрам.
Рассмотрим параболу  . Введем замену:
. Введем замену:  . Получим:
. Получим:  - уравнение множественной линейной регрессии. Парабола 2-й степени целесообразна к применению. Если для определенного интервала значений фактора меняется характер связи признаков: прямая связь меняется на обратную или наоборот. Кривая, для которой b > 0, c < 0 используется при изучении зависимости з/п работников физического труда от возраста. При b < 0, c > 0 – зависимость затрат на производство от объема выпуска. Часто можно использовать лишь сегмент параболы.
- уравнение множественной линейной регрессии. Парабола 2-й степени целесообразна к применению. Если для определенного интервала значений фактора меняется характер связи признаков: прямая связь меняется на обратную или наоборот. Кривая, для которой b > 0, c < 0 используется при изучении зависимости з/п работников физического труда от возраста. При b < 0, c > 0 – зависимость затрат на производство от объема выпуска. Часто можно использовать лишь сегмент параболы.
Аналогично линеаризуются полиномы любой степени. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.
Равносторонняя гипербола  может быть использована для характеристики связи удельных расходов сырья, материалов, топлива с объемами выпускаемой продукции, временем обращения товаров от величины товарооборота. Классическим примером является кривая Филлипса, характеризующая соотношение между нормой безработицы х и процентом прироста з/п у. После замены
может быть использована для характеристики связи удельных расходов сырья, материалов, топлива с объемами выпускаемой продукции, временем обращения товаров от величины товарооборота. Классическим примером является кривая Филлипса, характеризующая соотношение между нормой безработицы х и процентом прироста з/п у. После замены
z = 1/x получим  - уравнение парной линейной регрессии. При b > 0 - кривая Филипса, при b < 0, кривая Энгеля, характеризующая связь доли расходов на товары длительного пользования и общих сумм расходов (или доходов).
- уравнение парной линейной регрессии. При b > 0 - кривая Филипса, при b < 0, кривая Энгеля, характеризующая связь доли расходов на товары длительного пользования и общих сумм расходов (или доходов).
Аналогично линеаризуются и другие нелинейные по переменным функции.
Замечание. Если зависимость между х и у нелинейна, а её представили линейной зависимостью, то:
- по графику уравнения регрессии (для парной) и точкам корреляционного поля можно определить необходимость нелинейного описания зависимости;
- в случае множественной регрессии можно проанализировать остатки регрессии. Обычно они должны чередоваться «+» и «-», большие и малые. При нелинейной зависимости нет случайного чередования остатков.
Класс функций, нелинейных по параметрам, в свою очередь, делится на два типа:
- нелинейные модели внутренне линейные;
- нелинейные модели внутренне нелинейные.
Внутренне линейные модели могут быть приведены к линейному виду.
Например.
1)  - внутренне линейна, так как
- внутренне линейна, так как  - линейна по параметрам;
- линейна по параметрам;
2)  - внутренне нелинейна;
- внутренне нелинейна;
3)  - внутренне нелинейна;
- внутренне нелинейна;
4)  - внутренне линейна, так как
- внутренне линейна, так как  ;
;
5)  - внутренне линейна, так как
- внутренне линейна, так как  ;
;
5)  - логистическая функция – внутренне линейна –
- логистическая функция – внутренне линейна –
 ;
;  ;
;  .
.
Замечание: чтобы получить аддитивный случайный член в уравнении регрессии, необходимо в исходной модели иметь мультипликативную случайную составляющую. Чтобы t- и F- критерии были применимы, необходимо, чтобы преобразованный случайный член имел нормальное распределение, т.е. исходный – логарифмически нормальное распределение
(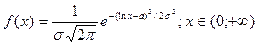 ).
).
Внутренне нелинейные модели не могут быть приведены к линейному виду, и для оценки их параметров используют итеративные процедуры.
Итеративные процедуры используют принцип минимизации суммы квадратов остатков и включают следующие шаги:
1. Принимаются некоторые правдоподобные значения параметров.
2. Вычисляются  по фактическим х.
по фактическим х.
3. Определяются  и
и  .
.
4. Вносятся небольшие изменения в оценки параметров.
5. Вычисляются новые  ,
, 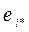 ,
,  .
.
6. Если  < S, то новые оценки лучше, их следует использовать в качестве новой отправной точки.
< S, то новые оценки лучше, их следует использовать в качестве новой отправной точки.
7. Шаги 4, 5, 6 повторяются до тех пор, пока окажется невозможным внести изменения, уменьшающие S.
8. Делается вывод о минимизации S, и последние оценки принимаются за оценки параметров.
Недостаток – медленное оценивание, однако в последнее время разработаны различные математические процедуры, позволяющие быстро находить приемлемое требуемое решение.