Полигон применяется чаще всего для изображения дискретных вариационных рядов распределения.
Пример
Имеется группировка сотрудников двух управлений одного из банков по размеру месячной заработной платы.
| № группы | Валютное управление | Кредитное управление | ||
| Размер заработной платы, тыс. руб. | Численность сотрудни ков, чел. | Размер заработной платы, тыс. руб. | Численность сотрудников, чел. | |
| до 10 | до 15 | |||
| 10-30 | 15-20 | |||
| 30-50 | 20-30 | |||
| 50-100 | 30-40 | |||
| 100-150 | 40-50 | |||
| 150 и более | 50-100 | |||
| 100-200 | ||||
| Итого |
Данные группировки сотрудников являются несопоставимыми, так как в приведенных группировках различные интервалы группировки и неодинаковое количество образованных групп.
Произведем вторичную группировку способом укрупнения интервалов:
| № группы | Размер заработной платы, тыс. руб. | Валютное управление | Кредитное управление | ||
| Численность сотрудников | Численность сотрудников | ||||
| Чел. | В % к итогу | Чел. | В % к итогу | ||
| до 30 | 7,81 | 4,85 | |||
| 30-50 | 18,75 | 38,57 | |||
| 50-100 | 56,25 | 34,29 | |||
| 100-150 | 17,19 | 22,29 | |||
| Итого | 100,00 | 100,00 |
При вторичной группировки способом долевой перегруппировки устанавливаем новые интервалы распределения работников по размеру месячной заработной платы, при этом за каждым интервалом закрепляем определенную долю единиц совокупности:
| № группы | Размер заработной платы, тыс. руб. | Валютное управление | Кредитное управление | ||
| Численность сотрудников | Численность сотрудников | ||||
| Чел. | В % к итогу | Чел. | В % к итогу | ||
| до 20 | 4,69 | 2,00 | |||
| 20-40 | 12,5 | 12,86 | |||
| 40-50 | 9,37 | 28,57 | |||
| 50-100 | 56,25 | 34,29 | |||
| 100-150 | 12,50 | 11,14 | |||
| 150 и более | 4,69 | 11,14 | |||
| Итого | 100,00 | 100,00 |
Результатом группировки является ряд распределения.
Ряд распределения – это ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку. Ряд распредлеения состоит из двух элементов: значение данного признака (варианта); вторая — число единиц с каждым значением признака (частота). Частоты, выраженные в виде относительных величин, отражающих долю каждой группы в общем объеме совокупности называют частостями.
В общем виде ряд распределения можно представить следующим образом:
Вариант 
| Частота 
|
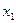
| 
|
| … | … |
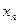
| 
|
| Итого | 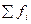
|
Классификация рядов распределения:
1. По характеру группировочного признака ряды распределения делят на две группы:
- атрибутивные ряды, которые построены на основе качественного признака.
- вариационные ряды - построены по количественному признаку.
По форме выражения признака вариационные ряды могут быть:
- Дискретные ряды – это ряды распределения, в которых признак выражен целым числом.
- Интервальные ряды, это вариационные ряды распределения, в которых признак выражен интервалом значений.
Дополнительную информацию при анализе статистисчеких рядов распределения можно получить при графическом изображении рядов распределения. Ряды распределения изображаются с помощью следующих видов графиков:
· Полигона
· Гистограммы
· Кумуляты
· Огивы.
При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.
Имеются данные о составе семей, проживающих на территории района:
| Семьи, состоящие из: | одного человека | двух человек | трех человек | 5 или более | всего |
| Доля группы в общем числе семей, в % | 19,2 | 26,2 | 22,6 | 20,5 | 100,0 |
Интервальные ряды распределения изображают графически в виде гистограммы.
Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).
Имеются данные о распределении 30 работников фирмы по размеру месячной заработной платы:
| Размер заработной платы руб. в месяц | Численность работников чел. |
| до 5000 | |
| 5000 — 7000 | |
| 7000 — 10000 | |
| 10000 — 15000 | |
| Итого: |
Задача: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты.
Решение:
1.Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
2.Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда. Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.
3.Построим гистограмму:
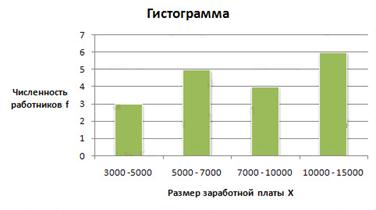
Кумулята или кумулятивная кривая строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости (рис. 6.3).
Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.
Рассчитаем накопленные частоты: наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.
| Размер заработной платы руб в месяц Xi | Численность работников чел. fi | Накопленные частоты S |
| до 5000 | ||
| 5000 — 7000 | ||
| 7000 — 10000 | ||
| 10000 — 15000 | ||
| Итого: | - |
При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:

Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.