Теоретическая часть

 

Пусть в попарноразличных точкаx x₀ , x₁..., x_n заданы значения f(x₀ ), f(x₁)..., f(x_n) приближенной функции f . Многочленом степени не выше n называют функцию вида

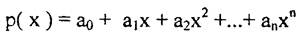(1)

 

построенную по набору узлов x₀, x₁..., x_n ,где а₀ , а₁..., а_n - вещественные константы

 

Представление интерполяционного многочлена P_n (x,f) в виде

многочлена Лагранжа:

 

, (2)

 

где

Интерполяционный многочлен (в том числе и Лагранжа) используется для нахождения ф-ии f в (.) . В качестве такого принимается точное значение такого многочлена при

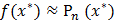(3)

 

Т.о. задача водится к вычислению значения интерполяционного многочлена

Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.