П.2 Подмножество. Основные числовые множества.

Опр.2.2.1 Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества.

Это записывается так: ВÌ А или АÉВ. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что m(В) £ m(А).

Знак Ì называется знаком включения.

Отметим основные свойства отношения включения между множествами:

1) ÆÌА для любого множества А;

2) АÌА для любого множества А (рефлексивность);

3) из того, что ВÌА не следует АÌВ (не симметричность);

4) если АÌВ и ВÌА, то А=В (антисимметричность);

5) если АÌВ и ВÌС, то АÌС (транзитивность).

Основные числовые множества:

N={1,2,3,4,…} – множество натуральных чисел;

Z={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все натуральные числа и числа, им противоположные), NÌZ;

Q={x ½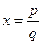, где pÎZ, qÎN} – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби), NÌZÌQ;

R=(-∞;+∞) – множество действительных чисел, QÌR (кроме всех рациональных чисел, содержит иррациональные числа, содержащие в своей записи знаки радикалов: ).