Интегрирование по частям

Замена переменной

Пример 1.

Пример 2.

Пример 3.

Пример 4.

 

Пример 1.Найти

Пример 2. Вычислить

Пример 3. Вычислите

Вычисление площадей плоских фигур.

 

Определение определенного интеграла как предела интегральной суммы позволяет получить различные формулы для нахождения площадей, длин и объемов геометрических объектов.

Пусть дана функция , , . Рассмотрим определенный интеграл от этой функции. С геометрической точки зрения определенный интеграл – это площадь под кривой

. (11)

 

Рис.1.

 

Площадь S находится по формуле: или находится из уравнения кривой.

II. Фигура расположена над осью и ограничена осью Ox, кривой () и двумя прямыми x = a и x = b (рис.2).

Рис. 2.

 

 

Пусть функция принимает как положительные, так и отрицательные значения, тогда площадь можно найти по формуле:

(12)

Рис. 3

Рис. 2.

Пусть дана функция , , где 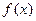, , , 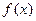. Тогда площадь ограниченная этими линиями определяется по формуле

, (13)

Рис. 5

Рис. 4.

Пример 1. Вычислить площадь, ограниченную графиками функций: