Метод интегрирования по частям

Пусть функции 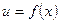и непрерывно дифференцируемые на некотором интервале. Имеет место тождество: .

Известно, что дифференциал произведения двух функций u(x), v(x) вычисляются по формуле:

d (uv) = udv + vdu

 

Интегрируя обе части, получим формулу интегрирования по частям или

Эта формула называется формулой интегрирования по частям.

 

Пример 1. Найти интеграл

Пример 2. Вычислить интеграл .