Выборочное наблюдение.
Наиболее совершенным и научно обоснованным способом несплошного наблюдения является выборочное наблюдение. При строгом соблюдении условий случайности и достаточно большой численности отобранных единиц выборочное наблюдение репрезентативно.
Способы формирования выборки:
1. Собственно случайный отбор: все единицы генеральной совокупности нумеруются, а выпавшие в результате жеребьевки номера соответствуют единицам, попавшим в выборку, причем число номеров равно запланированному объему выборки.
2. Механический отбор: отбираются единицы генеральной совокупности с постоянным шагом N/п.
3. Стратифицированный (расслоенным) отбор осуществляется из неоднородной генеральной совокупности, когда ее предварительно разбивают на однородные группы, после чего производят отбор единиц из каждой группы в выборочную совокупность случайный или механическим способом пропорционально их численности в генеральной совокупности.
4. Серийный (гнездовой)отбор: случайным или механическим способом выбирают не отдельные единицы, а определенные серии (гнезда), внутри которых производится сплошное наблюдение.
После завершения отбора необходимого числа единиц в выборку и регистрации предусмотренных программой наблюдения изучаемых признаков этих единиц, переходят к расчету обобщающих показателей. К ним относят среднюю величину изучаемого признака и долю единиц, обладающих каким-либо значением этого признака. Обобщающие характеристики, рассчитанные по данным выборки, будут отличаться от их реальных значений в генеральной совокупности, поэтому введем следующие условные обозначения (см.табл. 1).
Таблица 1. Условные обозначения
| Показатель | Совокупность | |
| генеральная | выборочная | |
| Число единиц совокупности | N | n |
| Среднее значение | 
| 
|
| Доля единиц, обладающих каким-либо значением признака | d | 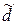
|
| Доля единиц, не обладающих каким-либо значением признака | 1-d | 1-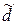
|
| Дисперсия | 
| 
|
Разность между значением обобщающих характеристик выборочной и генеральной совокупностей называется ошибкой выборки, которая подразделяется на ошибку регистрации и ошибку репрезентативности.
Для измерения ошибки выборки определяется ее средняя ошибка по формуле
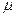 =
= 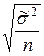 – для повторного отбора;
– для повторного отбора;
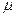 =
= 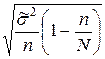 – для бесповторного отбора.
– для бесповторного отбора.
Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки  . Она определяется в долях средней ошибки с заданной вероятностью, т.е.
. Она определяется в долях средней ошибки с заданной вероятностью, т.е.
 = t
= t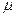 ,
,
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки.
Значения P (интеграла Лапласа) для разных t рассчитаны и имеются в специальной таблице. Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. Чаще всего принимают вероятность P = 0,950, которая означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы. Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения t и рассчитывают предельную ошибку выборки по формуле.
После расчета предельной ошибки находят доверительный интервал обобщающей характеристики генеральной совокупности по формуле – для среднего значения, и по формуле – для доли единиц, обладающих каким-либо значением признака:
 или (
или ( –
– )
)

 (
( +
+ )
)
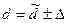 или (
или (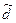 –
– )
) d
d  (
(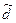 +
+ )
)
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики генеральной совокупности, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
При организации выборочного наблюдения возникает необходимость определения необходимой численности выборки для средней:
для повторной выборки n =  ; для бесповторной выборки n =
; для бесповторной выборки n =  .
.