Структурные средние

При изучении вариации применяются такие характеристики ряда распределения, которые описывают количественно его структуру, строение. Такова, например, медиана – величина варьирующего признака, делящая совокупность на две равные части – со значением признака меньше медианы и со значением признака больше медианы. В интервальном ряду распределения для нахождения медианы применяется формула:

,

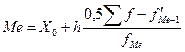где Ме – медиана;

X₀ – нижняя граница интервала, в котором находится медиана;

h – величина (размах) интервала;

– накопленная частота в интервале, предшествующем медианному;

f_Me – частота в медианном интервале.

Безусловно, важное значение имеет такая величина признака, которая встречается в изучаемом ряду распределения чаще всего. Такую величину принято называть модой. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. В интервальном ряду распределения интервал с наибольшей частотой является модальным. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения (число единиц совокупности, приходящихся на единицу измерения варьирующего признака) достигает максимума. Это условное значение и считается точечной модой:

,

где Мо – мода;

Х₀ – нижнее значение модального интервала;

f_Mo – частота в модальном интервале;

f_Mo-1 – частота в предыдущем интервале;

f_Mo+1 – частота в следующем интервале за модальным;

h – величина интервала.