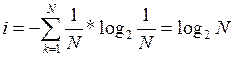Дополнительный материал

Существует общая формула вычисления количества информации для событий с различными вероятностями. Эту фор­мулу в 1948 году предложил американский математик и инженер Клод Шеннон. Ко­личество информации в этом случае вычисляется по формуле:

 

 

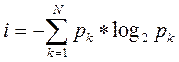
где: i - количество информации;

N - количество возможных событий;

P _k - вероятность отдельных событий.

Задача №3

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Сколько информации мы получим, когда поймаем какую-нибудь рыбу. Решение:

1. Найдем общее количество рыб в озере: S = 12500 + 25000 + 2-6250 = 50000.

2. Найдем вероятность попадания на удочку каждого вида рыб:
Ро= 12500/50000 = 0,25,

Pк = 25000 /50000 = 0,5,

Pп =6250/50000 = 0,125,

Pщ = 6250/50000 = 0,125.

3. Найдем количество информации:

i = - (0,25*log₂0,25 + 0,5*log₂0,5 + 0,125*log₂0,125 + 0,125*log₂0,125) = - (0,25*(-2) + 0,5*(-1) + 0,125*(-3) + 0,125*(-3)) =

= -(-0,5-0,5-0,375-0,375)= -(-1,75)= 1,75 бит.

Ответ: 1,75 бит информации.

 

 

Для равновероятных событий р_k = 1/N. Поэтому количество информации рассчитывается по следующей формуле: