Генеральная и выборочная совокупности.

Математическая статистика - это наука, которая, основываясь на методах теории вероятностей, занимается систематизацией и обработкой статистических данных для получения научных и практических выводов. Статистическими данныминазываются сведения о числе объектов, обладающих теми или иными признаками.

Группа объектов, объединенных по некоторому качественному или количественному признаку, называется статистической совокупностью. Объекты, входящие в совокупность, называются её элементами, а их общее число – ее объемом.

Генеральной совокупностью называется множество всех мыслимо возможных наблюдений, которые могли бы быть сделаны при данном реальном комплексе условий или более строго: генеральной совокупностью называется случайная величина x и связанное с ней вероятностное пространство {W,Á,Р}.

Распределение случайной величины x называют распределением генеральной совокупности (говорят, например, о нормально распределенной или просто нормальной генеральной совокупности).

Например, если производится ряд независимых измерений случайной величины x,то генеральная совокупность теоретически бесконечна (т.е. генеральная совокупность - абстрактное, условно - математическое понятие); если же проверяется число дефектных изделий в партии из N изделий, то эту партию рассматривают как конечную генеральную совокупность объема N. В случае социально-экономических исследований генеральной совокупностью объема N может быть население какого-то города, региона или страны, а измеряемыми признаками – доходы, расходы или объем сбережений отдельно взятого человека. Если какой-то признак имеет качественный характер (например, пол, национальность, социальное положение, род деятельности и т.п.), но принадлежит к конечному множеству вариантов, то он может быть также закодирован числом (как это часто делают в анкетах).

Если число объектов N достаточно велико, то провести сплошное обследование затруднительно, а иногда физически невозможно (например, проверить качество всех патронов). Тогда случайным образом отбирают из всей генеральной совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью или просто выборкой объема n называется последовательность х₁, х₂, …, х_n независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением случайной величины x.

Например, результаты n первых измерений случайной величины x принято рассматривать как выборку объема n из бесконечной генеральной совокупности. Полученные данные называют наблюдениями случайной величины x, а также говорят, что случайная величина x "принимает значения" х₁, х₂, …, х_n.

Основная задача математической статистики– сделать научно обоснованные выводы о распределении одной или более неизвестных случайных величин или их взаимосвязи между собой. Метод, состоящий в том, что на основании свойств и характеристик выборки делаются заключения о числовых характеристиках и законе распределения случайной величины (генеральной совокупности) называется выборочным методом

Для того, чтобы характеристики случайной величины, полученные выборочным методом, были объективны, необходимо, чтобы выборка была репрезентативной, т.е. достаточно хорошо представляла исследуемую величину. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно, т.е. все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку. Для этого существуют различные виды отбора выборки.

1. Простым случайным отбором называется отбор, при котором объекты извлекаются по одному из всей генеральной совокупности.

2. Стратифицированный (расслоенный) отбор заключается в том, что исходная генеральная совокупность объема N подразделяется на подмножества (страты) N₁,N₂,…,N_k, так что N₁+N₂+…+N_k=N. Когда страты определены, из каждого из них извлекается простая случайная выборка объема n₁,n₂,…,n_k. Частным случаем стратифицированного отбора является типический отбор, при котором объекты отбирают не из всей генеральной совокупности, а из каждой типической ее части.

Комбинированный отбор сочетает в себе сразу несколько видов отбора, образующих различные фазы выборочного обследования. Существуют и другие методы организации выборки.

Выборка называетсяповторной, если отобранный объект перед выбором следующего возвращается в генеральную совокупность. Выборка называется бесповторной, если отобранный объект в генеральную совокупность не возвращается. Для конечной генеральной совокупности случайный отбор без возвращения приводит на каждом шаге к зависимости отдельных наблюдений, случайный равновозможный выбор с возвращением – к независимости наблюдений. На практике обычно имеют дело с бесповторными выборками. Тем не менее, когда объем генеральной совокупности N во много раз больше, чем объем выборки n (например, в сотни или тысячи раз), зависимостью наблюдений можно пренебречь.

Таким образом, случайная выборка х₁, х₂, …, х_n – это результат последовательных и независимых наблюдений над случайной величиной ξ, представляющую генеральную совокупность, и все элементы выборки имеют тоже распределении, что исходная случайная величина x.

Функцию распределения F_x(х) и другие числовые характеристики случайной величины x будем называть теоретическими, в отличие от выборочных характеристик, которые определяются по результатам наблюдений.

Пусть выборка х₁,х₂,…,х_к есть результат независимых наблюдений случайной величины x, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раза, …, х_к - n_к раз, так что 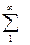n_i=n – объем выборки. Число n_i, показывающее, сколько раз появилось значение х_i в n наблюдениях, называется частотой данного значения, а отношение n_i/n=w_i – относительной частотой. Очевидно, что числа w_i рациональны и .

Статистическая совокупность, расположенная в порядке возрастания признака, называется вариационным рядом. Его члены обозначают x₍₁₎, x_(2), … x_(n) и называют вариантами. Вариационный ряд называется дискретным, если его члены принимают конкретные изолированные значения. Статистическим распределением выборки дискретной случайной величины x называется перечень вариант и соответствующих им относительных частот w_i . Полученная таблица называется статистическим рядом.

X(1)	x(2)	...	xk(k)
ω1	ω2	...	ωk

Наибольшее и наименьшее значения вариационного ряда обозначают x_min и x_max и называют крайними членами вариационного ряда.

Если изучается непрерывная случайная величина, то группировка заключается в разбиении интервала наблюдаемых значений на k частичных интервалов [c₀,c₁), [c₁,c₂), …, [c_k-1,c_k] равной длины h, и подсчете числа попаданий наблюдений в эти интервалы. Полученные числа принимают за частоты n_i (для некоторой новой, уже дискретной случайной величины). В качестве новых значений вариант x_i обычно берутся середины интервалов (либо в таблице указываются сами интервалы). Согласно формуле Стерждеса рекомендуемое число интервалов разбиения k»1+log₂n, а длины частичных интервалов равны h=(x_max-x_min)/k. Предполагается, что весь интервал имеет вид [x_min, x_max].

 

 

Графически статистические ряды могут быть представлены в виде полигона, гистограммы или графика накопленных частот.

Полигоном частотназывают ломаную линию, отрезки которой соединяют точки (x₁,n₁), (x₂,n₂), …, (x_k,n_k). Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁,w₁), (x₂,w₂), …, (x_k,w_k). Полигоны обычно служат для изображения выборки в случае дискретных случайных величин (рис.7.1.1).

Рис. 7.1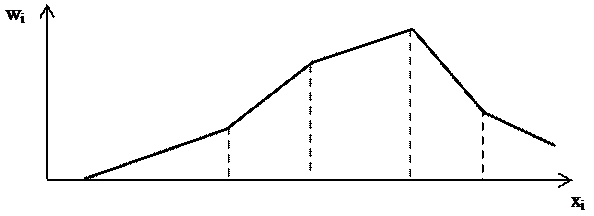
.1.

Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длиною h , а высоты

равны w_i/h.

Рис.7.1.2.

Гистограмма обычно служит для изображения выборки в случае непрерывных случайных величин. Площадь гистограммы равна единице (рис.7.1.2). Если на гистограмме относительных частот соединить середины верхних сторон прямоугольников, то полученная ломанная образует полигон относительных частот. Поэтому гистограмму можно рассматривать как график эмпирической (выборочной) плотности распределения f_n(x). Если у теоретического распределения существует конечная плотность, то эмпирическая плотность является некоторым приближением теоретической.

Графиком накопленных частот называется фигура, строящаяся аналогично гистограмме с той разницей, что для расчета высот прямоугольников берутся не простые, а накопленные относительные частоты,т.е. величины 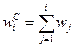. Эти величины не убывают, и график накопленных частот имеет вид ступенчатой "лестницы" (от 0 до 1).

График накопленных частот на практике используются для приближения теоретической функции распределения.

Задача. Анализируется выборка из 100 малых предприятий региона. Цель обследования – измерение коэффициента соотношения заемных и собственных средств (х_i) на каждом i–ом предприятии. Результаты представлены в таблице 7.1.1.

 

Таблица Коэффициенты соотношений заемных и собственных средств предприятий.

5,56	5,45	5,48	5,45	5,39	5,37	5,46	5,59	5,61	5,31
5,46	5,61	5,11	5,41	5.31	5,57	5,33	5,11	5,54	5,43
5,34	5,53	5,46	5,41	5,48	5,39	5,11	5,42	5,48	5,49
5,36	5,40	5,45	5,49	5,68	5,51	5,50	5,68	5,21	5,38
5,58	5,47	5,46	5,19	5,60	5,63	5,48	5,27	5,22	5,37
5,33	5,49	5,50	5,54	5,40	5.58	5,42	5,29	5,05	5,79
5,79	5,65	5,70	5,71	5,85	5,44	5,47	5,48	5,47	5,55
5,67	5,71	5,73	5,05	5,35	5,72	5,49	5,61	5,57	5,69
5,54	5,39	5,32	5,21	5,73	5,59	5,38	5,25	5,26	5,81
5,27	5,64	5,20	5,23	5,33	5,37	5,24	5,55	5,60	5,51

 

Построить гистограмму и график накопленных частот.

Решение. Построим группированный ряд наблюдений:

1. Определим в выборке х_min =5,05 и x_max= 5,85;

2. Разобьем весь диапазон [x_min, x_max] на k равных интервалов: k»1+log₂100=7,62; k=8, отсюда длина интервала

Таблица 7.1.2. Сгруппированный ряд наблюдений

Номер Интервала	Интервалы	Середины интервалов хi	wi		fn(x)
	5,05–5,15	5,1	0,05	0,05	0,5
	5,15–5,25	5,2	0,08	0,13	0,8
	5,25–5,35	5,3	0,12	0,25	1,2
	5,35–5,45	5,4	0,20	0,45	2,0
	5,45–5,55	5,5	0,26	0,71	2,6
	5,55–5,65	5,6	0,15	0,86	1,5
	5,65–5,75	5,7	0,10	0,96	1,0
	5,75–5,85	5,8	0,04	1,00	0,4

 

На рис. 7.1.3 и 7.1.4, построенных по данным таблицы 7.1.2, представлены гистограмма и график накопленных частот. Кривые соответствуют плотности и функции нормального распределения, "подобранного" к данным.

 

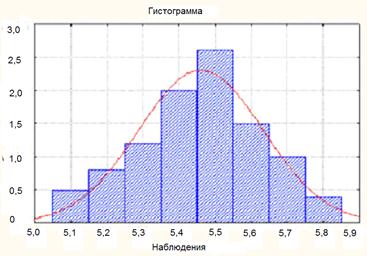
Рис. 7.1.3.

 

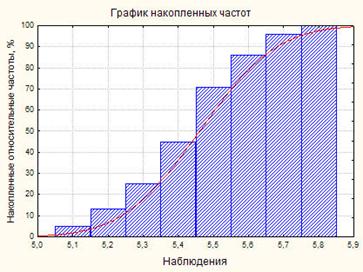
Рис. 7.1.4.

Таким образом, распределение выборки является некоторым приближением распределения генеральной совокупности.