Если делитель умножить на значение частного, то получим делимое.

Если значение произведения разделить на один множитель, то получим другой множитель.

Задания.

1. Сравни выражения в каждой паре, чем они похожи? Чем отличаются? Чем похожи все вторые выражения в каждой паре? Чем похожи первые выражения в каждой паре?

72–9–3+6 48–6+7+8 27–3+2–7

72:9•3:6 48:6•7:8 27:3•2:7

2. Догадайся! По какому признаку записаны выражения в каждом столбике?

29–8+24 72:9•3

32+9–7+14 48:6•7:8

64–7+16–8 27:3•2:6•9

3. Можно ли утверждать, что значение выражений в каждом столбике одинаковы?

56:7 54:9

7•8(32:4) 9•6:(36:4)

(65–9):(24:3) (72–18):(27:3)

4. Какие числа нужно вставить в «окошко» чтобы получить верное неравенство?

24+4•3= +24

5. Расставь порядок выполнения действий на каждой схеме:

1 + 1 : 1 + 1 • 1 - 1

1 • 1 + ( 1 +1) - 1

1 : 1 + 1 -1 - (1 +1)

1 - 1 • (1 +1) + 1 :1 -1

(1 -1) : (1 - 1) • ( 1+1) +1

(1 - 1) •1 +1 + (1 - 1) • 1 - 1 : 1

6. Вычисли:

(25–5):4+2 (13 • 2) + ( 4 • 3) (12 + 4) • (5 + 2) • (5 – 1)

 

Вопрос 10. Понятие уравнения с одной переменной. Равносильные уравнения. Теоремы о равносильности уравнений. Формирование представлений об уравнении в начальном курсе математики. Методика обучения решению простейших уравнений.

Возьмем 2 выражения с переменной: 4х и 5х+2, соединим их знаком равенства, получим предложение: 4х=5х+2. При х=–2 предложение обращается в истинное числовое равенство, а при х=1 – ложное. Предложение 4х=5х+2 – высказывательная форма. Ее называют уравнением с одной переменной.

Определение: Пусть f(х) и g(х) – два выражения с переменной х и областью определения Х. Тогда высказывательная форма вида f(х)=g(х)называется уравнением с одной переменной. Значение переменной «х» из множества Х, при котором уравнение обращается в истинное числовое равенство, называется корнем уравнения.Решить уравнение – это значит найти множество его корней. Следовательно, корнем уравнения 4х=5х+2 на множестве R действительных чисел является –2.

Чтобы решить какое-либо уравнение, его преобразовывают, заменяя более простым. Этот процесс продолжают до тех пор, пока не получают уравнение, корни которого можно найти известным способом. Два уравнения, множества корней которых совпадают, называют равносильными.

Определение: Два уравнения f₁(х)=g₁(х) и f₂(х)=g₂(х) называются равносильными, если множества их корней совпадают. Пример: уравнения х²–9=0 и (2х+6)•(х–3)=0 равносильны, так как имеют своими корнями числа 3 и –3. Для выяснения вопроса о видах преобразований, позволяющих получать равносильные уравнения, рассмотрим теоремы.

Теорема №1. Если к обеим частям уравнения прибавить одно и то же число или выражение, имеющее смысл, то получим уравнение, равносильное данному.

Следствие из Т1. Если какое-либо слагаемое перенести из одной части уравнения в другую, поменяв знак слагаемого на противоположный, то получим уравнение, равносильное данному.

Теорема №2. Если обе части уравнения с областью определения Х умножить на одно и то же число или выражение, которое определено на том же множестве и не обращается на нем в нуль, то получим уравнение равносильное данному.

Следствие из Т2. Если обе части уравнения умножить (или разделить) на одно и то же число или выражение, отличное от нуля, то получи уравнение, равносильное данному.

Пример: 6–2х=х

6=х+2х по Т1

6=3х : 3≠0 по Т2

х=2.

В курсе математики начальных классов уравнение рассматривается как истинное равенство, содержащее неизвестное число, и решается оно на основе правил взаимосвязи между компонентами и результатами арифметических действий. Этот вопрос изучается в традиционной образовательной системе по программе 1 – 4 в 3 классе на стр. 133. Вводится это понятие контекстуально – остенсивно. Даны 2 предложения +4=12 и х+4=12. Буквой х(икс) обозначено неизвестное число, которое надо найти. х+4=12 – это уравнение. Решим уравнение: узнаем, какое число надо представить вместо «х», чтобы равенство было верным. Это число 8, так как 8+4=12 – верное равенство.

Недостатки такого подхода: при введении понятия уравнения в данном виде не ясно по какой причине только предложение х+4=12 является уравнением. Следовательно, например, предложение 5–у=12 – не уравнение. Необходимо обговорить все возможные варианты, не только сумму, но и разность, произведение и частное.

Пример: d–4=10

17:х=17 все это уравнения

12ху=24

Так же необходимо вводить не только букву «х» для обозначения неизвестного, но и рассматривать другие буквы латинского алфавита. Знакомство младших школьников с понятием уравнения можно разделить на 3 этапа:

1 этап – подготовительный. Это примеры с окошками. Учащиеся решают данные примеры с помощью подбора. Вводятся с 1 кл. Пример: +2=10.

На данном этапе учащиеся учатся читать, записывать и решать данные выражения. Пример: Запиши. Если к неизвестному числу прибавить 2, то получим 10. Реши данный пример.

2 этап – В 3 классе вводятся буквенные обозначения. Так же решаются подбором. Пример х+7=14

На данном этапе вводится и существенные признаки: 1. Знак равенства.

На выделение существенных признаков необходимо прорешать систему упражнений (см. далее).

3 этап – Уравнение решаем на основе зависимости компонентов. По алгоритму:

o На какое действие данное уравнение?

o Назови компоненты этого действия?

o Какой компонент неизвестен?

o Как найти неизвестный компонент?

Важным является то, что учащихся надо приучить делать проверку. Пример.

Термин «решение» употребляется в 2-х смыслах:

ü Обозначает как число (корень), при подстановке которого уравнение обращается в верное числовое равенство;

ü Процесс отыскания этого числа, то есть способ решения уравнения.

Можно познакомить учащихся с уравнениями как можно раньше и в процессе их решения осуществлять работу по усвоению детьми правил о взаимосвязи компонентов и результатов действий. Можно приступать к решению уравнений после того, как учащиеся усвоят необходимую терминологию и те правила, которыми они будут пользоваться для решения уравнений. Для осознания взаимосвязи между компонентами и результатами арифметических действий, необходимо опираться на предметную деятельность. В противном случае при решении уравнений мы вынуждены идти через образ и большое количество тренировочных упражнений. Учащиеся руководствуются внешними признаками. Например, 8+х=6 – получаем от учащихся х=8–6, это наиболее распространенная ошибка. Более позднее изучение уравнений позволяет использовать в уравнениях многозначные числа и ранее изученные понятия.

Система упражнений:

1. Из данных выражений выдели уравнения.

а + 2 = 4

10 + 1 = 11

d – 4 = 17

2 + х = 13

14 - = 2

2. Придумайте свое уравнение.

3. Реши сказочные уравнения (2 кл.).

€ + 3 = 12 7 + €= 25

£ – 10 = 15 1000 – ¥= 5

4. Составь уравнение по схеме (3 кл.).

5. Объясни, почему уравнение соответствует данной схеме (3 кл.).

 

х + 40 = 56 + 32

 

6. По данному рисунку придумай задачу, которую можно записать уравнением (3 кл.).

40х=28•20

		40 см

 

 

Вопрос 11. Понятие отрезка натурального ряда чисел и счёта элементов конечного множества. Теоретико-множественный смысл натурального числа и нуля. Натуральное число как результат измерения величины. Определение отношения «меньше» для натуральных чисел, его теоретико-множественный смысл. Формирование у младших школьников представлений о счёте, порядковом и количественном числе, последовательности и названии чисел натурального ряда. Методика формирования у младших школьников понятий «меньше» и «больше» для натуральных чисел.

В аксиоматике раскрывается порядковый смысл натурального числа, но натуральные числа имеют и количественный смысл. Чтобы выяснить, как взаимосвязаны эти два смысла, рассмотрим такие понятия, как отрезок натурального ряда, счёт элементов конечного множества.

Определение: Отрезком N_a натурального ряда называется множество натуральных чисел, не превосходящих натурального числа . Таким образом, можно записать: N_a= {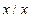и }. Например: Отрезок N₇ – множество натуральных чисел, не превосходящих числа 7, тот есть N₇ = {1, 2, 3, 4, 5, 6, 7}.

Отметим важные свойства отрезков натурального ряда:

1) любой отрезок N_a содержит единицу (свойство вытекает из определения отрезка N_a).

2) Если число содержится в отрезке N_a и , то и непосредственно следующее за ним число также содержится в N_a.

Определение: Множество A называется конечным, если оно равномощно некоторому отрезку N_a натурального ряда. Например: Множество A вершин треугольника – конечное множество, так как оно равномощно отрезку N₃= {1, 2, 3}, то есть A ~ N₃.

Определение: Если непустое конечное множество A равномощно отрезку N_a, то натуральное числоназывают числом элементов множества A и пишут n(A)=. Например: A – множество вершин четырёхугольника, то n (A)=4.

Определение: Установление взаимно однозначного соответствия между элементами непустого конечного дискретного множества A и отрезком натурального ряда называется счётом элементов множества A. Таким образом, всякое натуральное число можно рассматривать как характеристику численности некоторого конечного множества A. Натуральное число имеет при этом количественный смысл. С теоретико-множественной точки зрения, натуральное число – это общее свойство класса конечных равномощных множеств. Например: Натуральное число «три» – это общее свойство класса множеств, равномощных, например, множеству сторон треугольника.

Число «нуль» с теоретико-множественной позиции рассматривается как число элементов пустого множества: 0=n(Ø). Таким образом, натуральное число как характеристику количественного множества можно рассматривать с двух позиций:

1) как число элементов во множестве A, получаемых при счёте, то есть =n(A), причём A~N_a;

2) как общее свойство класса конечных равномощных дискретных множеств.

Натуральное число как результат измерения величины, показывает, из скольких мерок состоит величина, значение которой измеряется.

Связь между конечными множествами и натуральными числами позволяет дать теоретико-множественное истолкование отношения «меньше».

Число меньше числатогда и только тогда, когда при счёте числоназывают раньше числа. Данная трактовка позволяет сравнивать числа, опираясь на знание их места в натуральном ряду.

Число играет огромную роль в жизни людей, следовательно, необходимо раннее формирование числовых представлений у ребёнка. Слова – числительные ребёнок соотносит с определённым образом: 2 – глаза, 1- рот и т. д. Таким образом, натуральное число – это целостный наглядный образ, в котором он не выделяет единичных предметов, следовательно, на вопрос «сколько?» он может ответить, не владея операцией счёта. Ребёнок осознаёт количественную характеристику групп предметов, устанавливая взаимно однозначное соответствие между ними. Тогда количественная характеристика числа выражается в понятиях «больше», «меньше», «столько же». При обучении учащихся устанавливать взаимно однозначное соответствие можно использовать следующие приёмы:

1. наложение предметов одного множества на предметы другого;
2. расположение предметов одного множества под предметами другого;
3. образование пар.

Это подготавливает детей к сознательному овладению операцией счёта. Для овладения операцией счёта необходимо запомнить порядок слов – числительных. Эта деятельность выполняется по образцу в процессе однотипных упражнений, увеличивая количество пересчитываемых предметов. Выполнение данных упражнений приводит к непроизвольному запоминанию порядка слов – числительных. В 6-7 лет дети уже владеют этим навыком, однако, возможны и ошибки. Для усвоения и уточнения порядка слов – числительных при счёте можно использовать различные формулировки заданий. Анализируя картинки с точки зрения различных признаков предметов (цвет, форма, количество), учащиеся упражняются в счёте. Таким образом, операция счёта есть нумерация данных объектов в определённой последовательности.

После усвоения слов – числительных можно переходить к формированию операции счёта и к обозначению каждого числа (к цифрам). Необязательно ориентироваться на порядок чисел в натуральном ряду (точка зрения Н.Б. Истоминой). Учащиеся должны осознавать различия между числом и цифрой. Это является сложной задачей и для ребенка, и для учителя. Рекомендуется познакомить учащихся с другим обозначением чисел: I, II, III, IV и т.д. Необходимо понять связь между количественным и порядковым числом. Каждое число, названное при счёте – и количественное, и порядковое, так как указывает на порядок предмета при счёте, а количественное, так как указывает на количество всех перечисленных предметов. Усвоить разницу помогут задания, при выполнении которых нужно ответить на вопросы: «который по счёту?», «сколько?». Порядковая и количественная характеристики тесно связаны. Овладение учащимися операцией счёта предполагает усвоение порядка слов – числительных и определённых правил: первым при счёте может быть указан любой объект совокупности, важно, чтобы ему соответствовало числительное «один». Ни одному объекту нельзя поставить в соответствие два слова – числительных. Ни один объект не должен быть пропущен при счёте.

Таким образом. В основе формирования понятия «число» лежит:

· счёт предметов;

· общая характеристика класса эквивалентных множеств;

· установление взаимно однозначного соответствия.

Определим, какие задачи стоят перед учителем при изучении этой темы:

1. Научить образовывать числа первого десятка;
2. совершенствовать умение называть эти числа;
3. научить читать и записывать числа от 1 до 10;
4. систематизировать знания о составе чисел 1 – 10;
5. формировать представления о месте каждого числа в натуральном ряде.

Вопрос 12. Теоретико-множественный смысл суммы натуральных чисел, смысл суммы натуральных чисел, полученных в результате измерения величин. Ознакомление учащихся младших классов со смыслом сложения. Типы ситуаций с предметными множествами, раскрывающими смысл сложения.

Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Например, если множество А содержит 5 элементов, а множество В – 4 элемента и пересечение множеств А и В пусто, то число элементов в их объединении равно сумме 5+4.

Теорема: Пусть А и В – конечные множества, не имеющие общих элементов. Тогда их объединение тоже конечно, причем n(AÈB)=n(A) + n(B).

Из рассмотренной теоремы следует, что с теоретико-множественных позиций сумма натуральных чисел аи в представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а=n(А), в=n(В): а+в = n(А) + n(В) = n(АÈВ), если АÇВ=Æ

Взаимосвязь сложения целых неотрицательных чисел и объединения множеств позволяет также обосновать выбор действий при решении текстовых задач определенного вида. Выясним, например, почему следующая задача решается при помощи сложения: «Катя нашла 3 гриба, а Миша – 4. Сколько всего грибов нашли девочки?». В задаче рассматриваются три множества: множество А грибов Кати, множество В грибов Маши и множество, являющееся их объединением. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как n(A)=3, n(B)=4 и АÇВ=Æ, то n(АÈВ)=3 + 4. Сумма 3 + 4 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 3 + 4 =7. Следовательно, девочки нашли 7 грибов.

Выясним, кокой смысл имеет сумма натуральных чисел, полученных в результате измерения величин.

Теорема: Если отрезок х состоит из отрезков у и z и длины отрезков у и zвыражаются натуральными числами, то мера длины отрезка х равна сумме мер длин его частей.

Из этой теоремы следует, что сумму натуральных чисел аи в можно рассматривать как меру длины отрезка х, состоящего из отрезков у и z, мерами длин которых являются числа аи в:а+в=m_e(Y) + m_e(Z) = m_e(Y+Z). Аналогичный смысл имеет сумма натуральных чисел, полученных в результате измерения других положительных скалярных величин.

Покажем, как используется данный подход к обоснованию выбора действия сложения при решении текстовых задач: «В саду собрали 7 кг смородины и 3 кг малины. Сколько всего килограммов ягод собрали?»

В задаче две величины – масса смородины и масса малины. Известны их численные значения. Требуется найти численное значение массы, которая получится, если данные массы сложить. Для этого, согласно рассмотренной теореме, надо сложить численные значения массы смородины и массы малины, т.е. получить выражение 7 + 3. Это математическая модель данной задачи. Вычислив значение выражения 7 + 3, получим ответ на вопрос задачи.

При помощи сложения решаются также текстовые задачи, в которых величины связаны отношением «больше на» или «меньше на». Например: «Купили 3 кг моркови, а картофеля на 2 кг больше. Сколько килограммов картофеля купили?». В задаче речь идет о двух величинах – массе моркови и массе картофеля. Численное значение первой массы известно, а численное значение второй надо найти, зная, что картофеля на 2 кг больше, чем моркови. Если построить вспомогательную модель задачи, то можно сразу увидеть, что картофеля купили столько же, сколько моркови, и еще 2 кг, т.е. масса картофеля складывается из двух масс (3 кг и 2 кг), и чтобы найти ее численное значение, надо сложить численные значения масс – слагаемых. Получаем выражение 3 + 2, значение которого и будет ответом на вопрос задачи.

В курсе математики начальных классов находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел в соответствии с которыми сложение целых неотрицательных чисел связано с операцией объединения попарно пересекающихся конечных множеств. При этом теоретико-множественная терминология и символика не используются. Далее учащиеся интерпретируют предметные действия в виде графических и символических моделей и устанавливают соответствия между различными моделями. Основная цель – осознание предметного смысла числовых выражений и равенств. При формировании у детей представлений о сложении можно условно ориентироваться на следующие предметные ситуации:

Название ситуации	Модель	Пример
а) увеличение данного предметного множества на несколько предметов	оооо¬оо	У Коли было 4 марки. Ему подарили еще 2 марки. Покажи, сколько марок стало у Коли.	Дети выкладывают 4 марки (круга, квадрата, треугольника) и движением руки показывают, сколько марок было у Коли. Затем добавляют 2 марки и движением руки показывают, сколько марок стало у Коли. Далее предметное действие описывается математическими знаками, используя для этой цели цифры, знаки «плюс» и «равно» (4 + 2 = 6). Целесообразно уже на этом этапе употреблять термины «выражение» и «равенство».
б) увеличение на несколько предметов множества, равносильного данному	оооо оооо¬оо	В вазе лежало 4 груши, а апельсинов столько же и еще 2. Покажи, сколько апельсинов в вазе.	В процессе выполнения предметных действий, связанных с данной предметной ситуацией, у детей формируются представления о понятии «больше на», которые связаны с построением совокупности, равночисленной данной («взять столько же») и ее увеличении на несколько предметов («еще»). Совокупность, полученная в результате, является объединением совокупностей предметов, обозначаемых терминами «столько же» и «еще».
в) составление одного предметного множества из двух данных	оооо оо	У Коли было 4 марки. Ему подарили еще 2. Покажи, сколько марок стало у Коли.	Ситуацию вида а) фактически можно свести к ситуации в), рассматривая марки, которые были у Коли, как одно предметное множество, а марки, которые ему подарили, как другое предметное множество. Для разъяснения смысла сложения можно также опираться на представления детей о соотношение целого и его частей. В этом случае для приведенной ситуации все марки Коли (целое) будут состоять из двух частей: марки, которые у него «были», и марки, которые ему «подарили». Обозначая целое и части их числовыми значениями, дети получают выражение 4 + 2 или 4 + 2 = 6.

 

Практически работу по ознакомлению учащихся со смыслом сложения можно организовать так:

1.Подготовительная работа:

Может быть направлена на соотнесение числа и предметного множества и наоборот (учитель показывает определенное количество предметов, ученики называют цифру, которой можно их обозначить; учитель называет, показывает цифру, учащиеся составляют соответствующее предметное множество), повторение понятий «больше», «меньше», «столько же» (положите 5 О, под ними расположите столько Ñ, чтобы можно было сказать, что их меньше, чем О. Положите столько ð, чтобы можно было сказать, что их больше, чем О. Что можно сказать о Ñ и ð?; какие предметы изображены, сосчитайте их; о каких предметах можно сказать, что их «больше», «меньше», «столько же»?

Ñ Ñ Ñ Ñ ¶¶¶¶

О О О О О О %%%%

2.Объяснение нового

В учебнике Математика 1 класс (1-4) стр.21 для ознакомления учащихся со знаком «+» и смыслом сложения предлагается последовательно рассмотреть 3 сюжетные картинки и составить к каждой из них математическую модель. Работу можно построить следующим образом: – Что изображено на 1-ой картинке? (1 кошка). – Как записать это на языке математики? (цифрой «1») (учитель записывает на доске).

– Что изменилось на следующей картинке? (пришла еще одна кошка). – Как обозначить количество пришедших кошек? (число 1) (учитель записывает рядом с числом 1 еще число 1) Можно ли по этой записи определить, увеличилось или уменьшилось количество кошек? (нет). Увеличение некоторого количества предметов называется сложением. Это действие обозначается знаком «+» (учитель записывает на доске 1+1). Эта запись читается так: «к одному прибавить один». – Что изображено на последней картинке? (2 кошки). – Как это записать? (числом 2). Чтобы показать на языке математики, что к 1 прибавить 1 получится 2, используем знак «=».

3.Система закрепляющих упражнений.

Для закрепления изученного материала можно использовать следующие задания:

1) соотнесение предметных действий с математическими записями:

У Димы было 2 ручки. Еще одну ручку ему дал брат. Сколько ручек стало у Димы?

Ученик выполняет предметные действия у доски и выбирает, какое из предложенных математических записей к ним подходит: 2 – 1 = 1; 3 – 1 = 2; 2 + 1 = 3; 3 – 2 = 1

2) соотнесение математической записи с графическими моделями

 

О О ¬ 2 + 3 = 5 О О О

“

¬ “ 2 + 1 = 3

“

 

3) заполнение окошек в выражениях и равенствах на основе анализа предложенных сюжетных картинок (с.23, 24) – Сколько белочек на левой картинке? (2). Как обозначено их количество? – Что произошло с белочками? (пришла еще 1). Как записать, что белочек стало на 1 больше? Прочитайте эту запись (к 2 прибавить 1).

4) чтение математических выражений и равенств и создание на их основе предметных ситуаций.

Прочитайте запись. Придумайте ситуацию, которую можно записать этой записью.

1 +1 = 2 2 + 1 = 3

5) создание на основе сюжетной картинки графической, а затем и математической модели:

___ ^^^^^ О О О “ “ “ “ “ 3+5=8

Следует добавить, что изучение смысла сложения и вычитания происходит параллельно. Поэтому можно использовать в данных заданиях как ситуации связанные со сложением, так и с вычитанием.

Вопрос 13. Теоретико-множественный смысл разности натуральных чисел. Условие существования разности на множестве натуральных чисел. Смысл разности натуральных чисел, полученных в результате измерения величин. Ознакомление учащихся младших классов со смыслом вычитания. Типы ситуаций с предметными действиями, раскрывающие смысл вычитания.

С теоретико-множественных позиций разность натуральных чисел a и b представляет собой число элементов в дополнении множества B до множества A, если a=n(A), b=n(B) и BÌA:

a–b = n(A) – n(B) = n(A\B), если BÌA

Пример: Объясним, используя данное определение, что 8 – 3 = 5. 8 = n(A), 3 = n(B), причем BÌA. Возьмем, например, множества A={1, 2, 3, 4, 5, 6, 7, 8}, B={1, 2, 3} => A\B={4, 5, 6, 7, 8,} => n(A\B)=5 => 8 – 3 = 5. Очевидно, что в качестве множеств A и B можно выбрать множества, отличные от рассматриваемых, поскольку разность a –b не зависит от выбора множеств A и B, удовлетворяющих условиям n(A) = a, n(B) = b и BÌA.

Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении задач. Выясним, например, почему следующая задача решается при помощи вычитания: «В аквариуме живет 7 рыбок, из них 4 золотые рыбки, остальные – сомики. Сколько сомиков живет в аквариуме?». В задаче рассматриваются 3 множества: A – множество всех рыбок, B – множество золотых рыбок, C = B\A – множество сомиков. В задаче требуется найти число элементов в этом дополнении. Т.к. по условию n(A) = 7, n(B) = 4 и BÌA, то n(C) = n(A\B) = n(A)–n(B) = 7– 4. Разность 7– 4 – математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 7– 4 = 3 => в аквариуме живет 3 сомика.

Разность натуральных чисел существует не всегда, т.к. BÌA => n(B) <n(A) => a – b натуральных чисел, таких, что a=n(A), b=n(B) и BÌA, существует тогда и только тогда, когда b<a. Действие, при помощи которого находят разность a-b – вычитание, a – уменьшаемое, b – вычитаемое. Действие вычитания является обратным сложению, а разность натуральных чисел a и b можно определить, как такое натуральное число c, сумма которого и числа b равна a

Выясним теперь, какой смысл приобретает вычитание натуральных чисел, если эти числа получены в результате измерения величин. Например, длины отрезка. Пусть отрезок а состоит из отрезков b и c и длинны отрезков а и b выражаются натуральными числами m_e и n_e (е – мерка), то значение длины отрезка с равно разности значений длин отрезков a и b: c = m_e – n_e, т.е. разность натуральных чисел m – n можно рассматривать как значение длины отрезка c, являющейся разностью длин отрезков a и b, выраженных натуральными числами m и n соответственно. Подход к вычитанию натуральных чисел связан не только с измерением длин отрезков, но и с измерением других величин.

В учебниках математики для начальных классов много задач, в которых рассматриваются различные величины и действия над ними. Определение смысла вычитания натуральных чисел, являющихся значениями величин, позволяет обосновать выбор действия при решении таких задач.

Например, рассмотрим задачу: «Масса гуся 7 кг, а кролик на 3 кг легче. Узнай массу кролика». В задаче рассматривается величина – масса. Е = 1 кг. m_e = 7 – численное значение массы гуся, n_e = 3 – численное значение дополнения к массе кролика до массы гуся. Необходимо найти численное значение массы кролика – с, по определению, численное значение массы кролика с = m_e – n_e = 7 – 3 = 4.

В начальном курсе математики первоначально вычитание целых неотрицательных чисел рассматривается на основе практических упражнений, связанных с выделением подмножества данного множества и образованием нового множества – дополнения выделенного подмножества, при этом теоретико-множественная терминология и символика не используется. Далее учащиеся интерпретируют предметные действия в виде графических и символических моделей и устанавливают соответствие между различными моделями. Основная цель – осознание предметного смысла числовых выражений и равенств.

При формировании у детей представлений о вычитании можно условно ориентироваться на следующие предметные ситуации.

Название ситуации	Модель	Пример
I. Уменьшение данного предметного множества на несколько предметов		У Маши было 5 шаров. 2 она подарила Тане. Покажи шары, которые у Маши остались.	Для разъяснения смысла вычитания можно использовать представление детей о соотношении целого и части. В этом случае шары, которые были у Маши («целое»), состоят из 2 частей: «Шары, которые она подарила и шары, которые у нее остались». Часть всегда меньше целого, поэтому нахождение части связано с вычитанием. Обозначая целое и части их числовыми значениями, дети получают выражение 6 – 2 или равенство 6–2=4
II. Уменьшение множества, равночисленного данному, на несколько предметов.		В вазе лежало 5 груш, а апельсинов столько же, но без 2. Покажи сколько апельсинов в вазе?	В процессе выполнения предметных действий, связанных с данной предметной ситуацией, у детей формируются представления о понятии «меньше на», которые связаны с построением совокупности, равночисленной данной («взять столько же») и ее уменьшением на несколько предметов («без»). В этом случае совокупность, обозначаемая термином «без», включается в совокупность, обозначаемую термином «столько же». Совокупность, полученная в результате вычитания, является дополнением до совокупности предметов, обозначаемой термином «столько же».
III. сравнение двух предметных множеств, т.е. ответить на вопрос: На сколько предметов в одном множестве больше (меньше) чем в другом?»		В каком ряду кругов больше? На сколько?	При рассмотрении данной ситуации детям предлагается установить взаимно однозначное соответствие между элементами 2х пре-дметных множеств на основе практических действий, удаление парных элементов, а затем ответить на вопрос: «В каком множестве элементов больше?» Далее учащимся предлагается решить ту же задачу без опоры на наглядность. В результате у учащихся формируется представление о разностном сравнении чисел, которое можно обобщить в виде правила: чтобы узнать, насколько одно число больше (меньше) другого, можно из большего числа вычесть меньшее.

 

Практически работу по ознакомлению учащихся со смыслом вычитания можно организовать так:

1. Подготовительная работа.

Может быть направлена на соотношение числа и предметного множества. И наоборот. Учитель показывает определенное количество предметов 1 или 2, ученики называют цифру, которой можно его обозначить; учитель называет, показывает цифру, учащиеся составляют соответствующее ей предметное множество. Повторение понятий «больше», «меньше», «столько же» (положите 5 кружков, под ними расположите столько треугольников, чтобы можно было сказать, что их меньше, чем кружков, положите столько четырехугольников, чтобы можно было сказать, что их больше, чем кружков. Что можно сказать о и ?; Какие предметы изображены, сосчитайте их; о каких предметах можно сказать что их «больше», «меньше», «столько же».

 

 

2. Объяснение нового.

В учебнике М1(1-4) стр. 21 для ознакомления учащихся со знаком "–" и смыслом вычитания предлагается последовательно рассмотреть 3 сюжетные картинки и составить к каждой из них математическую модель. Работу можно построить следующим образом. Что изображено на 1-ой картинке? (2 воробья). Как записать это на языке математики? (цифрой 2, учитель записывает на доске). Что изменилось на следующей картинке? (1 воробей улетел). Как обозначить количество улетевших воробьев? (числом 1, учитель записывает рядом с числом 2 число 1). Можно ли по этой записи определить, увеличилось ли количество воробьев или уменьшилось? (нет). Уменьшение некоторого количества предметов на несколько предметов называется вычитанием. Это действие обозначается знаком "–" (учитель записывает на доске 2–1). Эта запись читается так: из 2 вычесть 1. Что изображено на следующей картинке? (1 воробей остался). Как это записать? (1). Это можно обозначить знаком "=" (из 2 вычесть 1 получится 1).

3. Закрепление.

Для закрепления изученного материала можно использовать следующие задания:

1) Соотнесение предметных действий с математическими записями.

Было 3 , 2 убрали. Сколько осталось?

(Ученик выполняет предметные действия у доски и выбирает, какая из предложенных математических записей к ним подходит.). 2+1=3, 3–1=2, 2–1=1, 3–2=1

Ученик должен не только соотнести ситуацию и ее запись, но и правильно прочитать запись

У Светы было 2 яблока, одно она отдала Маше. Сколько яблок осталось у Светы? 2–1=1

2) Соотнесение математической записи с графическими моделями.

 

 

3) Заполнение окошек в выражениях и равенствах на основе анализа предложенных сюжетных картинок (стр. 23, стр. 25).

Сколько зайчиков на левой картинке? (3). Верно ли обозначено их количество? Что изменилось на следующей картинке? (2 ушли). Как записали, что зайцев стало 3 без 2 (на 2 меньше)? Прочитайте эту запись (из 3 вычесть 2). Сколько зайчиков осталось, запишите это? (1)

Пользуясь рисунком вставьте числа в «окошки».

____

 

 

4) Чтение математических выражений и равенств. И создание на их основе предметных ситуаций.

Прочитай запись. Придумай ситуацию, которую можно определить этой записью.

3–2=1 3–1=2

5) Создание на основе сюжетной картинки графической, а затем и математической модели.

 

Следует добавить, что изучения смысла сложения и вычитания происходит параллельно, поэтому можно использовать в данных записях как ситуации, связанные с вычитанием, так и со сложением. Понимание учащимися смысла вычитания очень важно, т.к. создает основу для дальнейшего изучения арифметического материала.

 

Вопрос 14. Определение умножения натуральных чисел через сложение, его теоретико-множественный смысл. Смысл произведения натуральных чисел, полученных в результате измерения величин. Методика ознакомления учащихся начальных классов со смыслом умножения целых неотрицательных чисел.

В начальной школе умножение рассматривается как сложение одинаковых слагаемых, что соответствует следующему определению: Если а,b – целые неотрицательные числа, то произведением a b называется число, удовлетворяющее следующим условиям:

1) а • b = а + а + … + а, если b>1

b слагаемых

2) а • b = а, если b=1

3) a • b = 0, если b=0

Случаю 1) этого определения можно дать теоретико-множественную трактовку. Если множества А₁, А₂,…,А_b имеют по а элементов, то их объединение А₁ È А₂ È … È А_b содержит a • b элементов. ТО, с точки зрения теоретико-множественной трактовки произведение a • b (b>1) представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются.

а • b = n(A₁ È A₂ È … È A_b), если n(А₁)=n(A₂)= … =n(A_b)=a и А₁, А₂,…,А_b попарно не пересекаются.

Можно дать другое теоретико-множественное истолкование произведения целых неотрицательных чисел. Оно связано с понятием декартова произведения множеств.

Теорема.Пусть А и B – конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство: n(AхB)= n(A) х n(B).

Из рассмотренной теоремы следует, что с теоретико-множественной точки зрения произведение а • b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что n(A)=a, n(B)=b, а • b = n(A) х n(B) = n(AхB)

Рассматривая смысл умножения натуральных чисел, являющихся мерами величин, возникает вопрос: с каким действием над величинами связано умножение натуральных чисел? Что бы ответить на него, проанализируем задачу: Купили 3 пакета муки по 2 кг в каждом. Сколько кг муки купили? В этой задаче речь идет о массе муки, которая сначала измерена пакетами, и известно численное значение этой массы при указанной единице массы. Требуется найти результат измерения той же массы муки, но при помощи другой единицы – килограмма при условии, что 1 пакет – это 2 кг муки. Рассуждения, связанные с поиском численного значения, массы муки при единице – кг, можно представить в таком виде: 3пак.=3х1пак.=3х(2кг)=3х2кг =(3х2)кг. Видим, что ответ на вопрос задачи находится умножением, и что оно оказалось связанным с переходом (в процессе измерения массы) от одной единицы массы к другой, более мелкой.

Теорема. Если отрезок х состоит из а отрезков, длина которого равна Е, а отрезок длины Е состоит из b отрезков, длина которых равна Е₁, то мера длины отрезка х при единице длины Е₁ равна а х b.

Из этой теоремы следует, что умножение натуральных чисел связано с переходом в процессе измерения к новой единице длины: если натуральное число а – мера длины отрезка Х при единице длины Е, натуральное число b – мера длины Е при единице длины Е₁, то произведение а • b – это мера длины отрезка х при единице длины Е₁: а • b = m_Е(Х) m_Е(Е)= m_Е(Х)

Аналогичный смысл имеет произведение натуральных чисел, полученных в результате измерения других (положительных) скалярных величин.

Данный вопрос в традиционной образовательной системе (1-4) изучается во 2 классе. Для подготовки учащихся к усвоению смысла умножения целых неотрицательных чисел, целесообразно вести счет групп предметов. Например: считай двойками, считай тройками и т.д. А так же предлагать задачи (примеры) на нахождение суммы одинаковых и неодинаковых слагаемых.

Например:

1) В трех коробках лежит по 6 карандашей в каждой. Сколько всего карандашей в коробках?

2) В первой коробке 3 карандаша, во второй – 6, в третьей – 8. сколько всего карандашей в коробках?

Подобные задачи полезно иллюстрировать предметными рисунками. Решая такие задачи и примеры, учащиеся замечают, что есть суммы с одинаковыми слагаемыми, и считают, сколько таких слагаемых. Затем сумма одинаковых слагаемых заменяется произведением (6+6+6+6=24; 6 • 4=24). Выполняя эту операцию, дети знакомятся с действием умножения, записью умножения, усваивают роль множителей.

Пример. Девочка наклеила марки на 4 страницы альбома по 5 марок на каждую. Сколько всего марок наклеила девочка? Учащиеся записывают решение: 5+5+5+5=20 Что можно сказать о слагаемых этой суммы? (они одинаковые). Сколько их?(4). Здесь по 5 взяли 4 раза. Если слагаемые одинаковые, то сумму можно записать иначе: 5 • 4=20. Читают эту запись так: по 5 взяли 4 раза, получили 20. здесь выполнили действие умножения. Сложение одинаковых слагаемых называется умножением. Умножение обозначается знаком (•). Что показывает в этой записи число 5? (число 5 – слагаемое). Что показывает число 4? (сколько раз взяли слагаемым число 5).

Умножение целых неотрицательных чисел можно ввести иначе: при помощи предметных действий, что позволяет для усвоения нового понятия активно использовать ранее изучаемый материал.

Учащимся предлагается схематический рисунок поля прямоугольной формы, которое разбито на равные части (квадраты). Нужно определить, на сколько участков (квадратов) разбито данное поле. Учащиеся, естественно, начинают действовать способом поединичного счета клеток, но скоро обнаруживают трудоемкость такой работы. Учитель ставит задачу: найти более простой путь поиска ответа. Достаточно посчитать число квадратов в одном ряду (9) и повторить это число слагаемым 6 раз (9+9+9+9+9+9). После этого учитель вводит новую запись: 9 • 6=54 и предлагает сопоставить эти две записи. Выясняется, что обозначает во втором равенстве первый множитель (какие слагаемые складываются) и второй множитель (сколько таких слагаемых).

Проверить усвоение смысла умножения целых неотрицательных чисел можно при помощи следующей системы закрепляющих упражнений:

1) замени, где возможно, сложение умножением:

7+7+7+7 19+19+119

3+3+13+3+13 0+0+0+0

8+8+8 1+1+1+1+1+11

2) замени умножение сложением:

6 • 5, 9 • 2, 3 • 8

3) выбери рисунок, который соответствует записи 2 • 6

4) не вычисляя значений произведений, поставь знаки < или >, чтобы получить верные неравенства:

12 • 9 … 12 • 11

24 • 7 … 24 • 5

5) можно ли, не вычисляя произведений, ответить на вопрос: на сколько значение первого произведения в каждом столбике меньше значения второго произведения?

6 • 4 5 • 3 7 • 8 6 • 3 7 • 2

6 • 5 5 • 4 7 • 9 6 • 5 7 • 4

6) вычисли значения произведений в каждом столбике, пользуясь данным равенством:

9 • 5=45 8 • 7=56 7 • 6 =42

9 • 4 8 • 6 7 • 5

9 • 6 8 • 8 7 • 7

 

Вопрос 15. Теоретико-множественный смысл частного натуральных чисел. Условие существования частного натуральных чисел. Смысл частного натуральных чисел, полученных в результате измерения величин. Методика ознакомления учащихся начальных классов со смыслом деления натуральных чисел.

В аксиоматической теории деление рассматривается как операция, обратная умножению, таким образом между делением и умножением устанавливается тесная взаимосвязь. Если а•в=с, то, зная произведение с и один из множителей, можно при помощи деления найти другой множитель. Если а•в=с, то а=с:в, в=с:а.

Выясним теоретико-множественный смысл полученных частных с:в и с:а. Произведение а•в=с – это число элементов в объединении впопарно непересекающихся множеств, в каждом из которых содержится аэлементов, т. е. с = а•в=n(А₁ÈА₂È_…ÈА_в ), где n(А₁)= n (А₂)=…=n(А_в). Т.к. множества А₁, А₂,…, А_в попарно не пересекаются, а при их объединении получается множество А, в котором с элементов, то можно говорить о разбиении множества А на равночисленные подмножества А₁, А_2,…, А_в. Тогда частное с:а – это число подмножеств в разбиении множества А, а частное с:в– число элементов в каждом подмножестве этого разбиения. Т.о., если а=n(A) и множество А разбито на попарно непересекающиеся подмножества и если:

в – число элементов в каждом подмножестве, то частное а:в – это число таких подмножеств;

в – число подмножеств, то частное а:в – это число элементов в каждом подмножестве.

Например: «12 карандашей разложили в 3 коробки поровну. Сколько карандашей в каждой коробке?» и «12 карандашей надо разложить в коробки по 3 карандаша в каждую. Сколько надо коробок?».

Для того чтобы существовало частное двух натуральных чисел а и b, необходимо, чтобы b≤a. Если частное натуральных чисел а и b существует, то оно единственно.

Выясним теперь смысл частного, полученного в результате измерения величин. Рассмотрим задачу: «6 кг муки надо разложить в пакеты по 2 кг в каждый. Сколько понадобится пакетов?». В задаче рассматривается масса муки, которая сначала измерена при помощи единицы массы – кг, и известно численное значение этой массы. Требуется найти результат измерения этой же массы, но уже при помощи другой единицы – пакета, причем известно, что 1п.=2кг; 1кг=½ п.=½ • (1п.); 6кг=6•1кг=6•(½ п.)=(6•½)•1 п.=(6:2) п.

Ответ на вопрос задачи находится делением, и оно связано с переходом от одной единицы массы к другой.

Теорема: Если отрезок хсостоит из а отрезков, длина которых равна Е, а отрезок длины Е₁ состоит из в отрезков длины Е, то мера длины отрезка х при единице длины Е₁ равна а:в.

Если натуральное число а – мера длины отрезка х при единице длины Е, а натуральное число в – мера новой единицы длины Е₁ при единице длины Е, то частное а:в– это мера длины отрезка х при единице длины Е₁: а:в=м_Е (х):м_Е (Е₁)=м_Е(х). Например: «Из 12м ткани сшили платья, расходуя на каждое по 4м. Сколько платьев сшили?». 12м=12•1 м=12•(¼ пл.)=(12•¼) пл.=(12:4) пл.

В традиционной образовательной системе 1-4 этот вопрос изучается во 2 классе. Деление как алгебраическая операция вводится на основе предметных действий. Основой формирования у младших школьников представления о смысле деления служит теоретико-множественный подход к трактовке частного, суть которого сводится к разбиению конечных множеств на равночисленные подмножества, не имеющие общих элементов. Этот подход позволяет опираться на жизненный опыт ребенка при введении новой терминологии и математической записи. Например: « Раздали 10 яблок по 2 каждой девочке. Сколько яблок получила каждая девочка?». Получить ответ на вопрос ребенку помогает наглядное изображение.

šš šš šš šš šš šš. На языке ребенка это означает, что он разделил все яблоки на части по два яблока в каждой, т.е. узнал, «сколько раз по два содержится в 10». Математическая запись: 10:2=5. Доступно и такое задание: «Раздай 10 яблок двум девочкам поровну».

а) одни будут брать по одному яблоку и раздавать девочкам по очереди, пока не раздадут все;

б) другие могут брать по два яблока и делить их между девочками, пока не раздадут все.

Можно использовать рисунок для того, чтобы учащиеся осознали результат выполненного предметного действия. ššššš ššššš.

Первый случай (5 частей по 2 яблока) – деление по содержанию. Второй (2 части по 5 яблок) – деление на равные части.

В практике сначала рассматривается первый случай, затем второй. Можно ввести соответствующие термины. В первом случае нужно говорить «10 разделили по 2», а во втором – « 10 разделили на 2».

Есть и другой подход, когда учащиеся устанавливают смысл деления не в процессе решения простых задач, а устанавливая соответствие между предметными моделями и математической записью (М₂)

š š š š

š š š š

š š š š

1. 2.

š š š š

š š š š

š š š š

Необходимо выяснить, чем похожи и чем отличаются картинки (в каждой 12 кружков, они разделены на части, в каждой части одинаковое количество кружков. Части равны). Это позволяет им самостоятельно выполнить рисунки других способов деления 12 кругов на равные части:

3. 4. 5.

š š š š š š

š š š š š š

š š	š š	š š
š š	š š	š š

š	š	š	š
š	š	š	š
š	š	š	š

 

Последующая работа сводится к выбору выражения, соответствующего каждой картинке.

Например, выражение 12:4 соответствует 1. и 2. картинкам.

В результате такой деятельности у детей формируется представление о предметном смысле деления.

Система закрепляющих упражнений может включать следующие задания:

1. Сравни рисунки в каждой паре и объясни, что обозначает каждое число в данных равенствах.

š š

š š

š š

š š

ššššš

ššššš 10:2=5 8:2=4

 

2. Какому рисунку соответствуют 3 выражения:

2•6 12:2 12:6

а) ššššš½ššššš½ššššš

б) šššš½šššš

в) šš½šš½šš½šš½šš½šš

 

3. Сделай рисунок, к которому можно записать 3 выражения:

а) 5•4, 20:4, 20:5

б) 4•5, 20:4, 20:5

 

Запиши к каждому рисунку 3 выражения:

а) šššššššš½šššššššš

б) šš½šš½šš½šš½šš½šš½šš½šš

 

В процессе выполнения заданий учащиеся осознают связь умножения и деления, которая обобщается в виде правил: