Доказательства

Свойства операций над отношениями

Приведем здесь список основных свойств операций над отношениями и докажем некоторые из них.

1) 2)

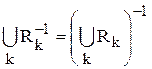
3) (R₁o R₂)^–1 = R₁^–1o R₂^–1. 4) (R₁o R₂) o R₃= R₁o (R₂o R₃).

5) (R₁È R₂) o R₃= (R₁o R₃) È ( R₂o R₃).

6) (R₁Ç R₂) o R₃Í (R₁o R₃) Ç ( R₂o R₃).

7) а) если R₁Í R₂ то R₁o R₃Í R₂o R₃;

б) если R₁Í R₂ то R₃o R₁Í R₃o R₂;

в) если R₁Í R₂ то R₁^–1Í R₂^–1.

8) a) (R₁È R₂)^d= R₁^dÇ R₂^d; б) (R₁Ç R₂)^d = R₁^dÈ R₂^d; в) (R^d)^d= R.

Свойство 2.

Пусть пара (x, y)Î(È R_k ) ^–1. Тогда (y, x)ÎÈ R_k. Это означает, что найдется отношение R_j, что (y, x)Î R_j. Отсюда, по определению обратного отношения, (x, y)ÎR_j^–1, а значит, (x, y)ÎÈR_k^–1и (ÈR_k)^–1Í È R_k^–1.

Докажем обратное включение. Пусть (x,y)Î R_k^–1 Это означает, что найдется такое множество R_j, что (x,y)ÎR_j^–1. Следовательно, (y, x)ÎR_j и (y, x)Î ÈR_k , поэтому (x, y)Î(È R_k )^–1. Значит, È R_k^–1Í (ÈR_k)^–1.

Одновременное выполнение обоих включений означает равенство множеств, что и требовалось доказать.

Свойство 6.

Пусть (x, y)Î(R₁ Ç R₂) o R₃. По определению композиции это означает, что найдется такое zÎA, что (x, z)Î(R₁Ç R₂) и (z, y)ÎR₃. Первое включение возможно только тогда, когда одновременно выполнено (x, z)ÎR₁ и (x, z)ÎR₂. Это, в свою очередь, означает, с учетом (z, y)ÎR₃, что одновременно (x, y)Î R₁o R₃ и (x, y)ÎR₂o R₃, а, следовательно, (x, y)Î(R₁o R₃) Ç (R₂o R₃), что и доказывает требуемое соотношение.

Замечание. Покажем, почему неверно обратное включение. Пусть (x, y) Î(R₁o R₃) Ç (R₂o R₃), тогда (x, y) Î(R₁o R₃) и (x, y) Î(R₂o R₃). Первое включение означает существование такого элемента z₁ из A, что (x, z₁)ÎR₁и (z₁, y) ÎR₃; второе – существование такого z₂ÎA, что (x, z₂)ÎR₂ и (z₂, y)ÎR₃, причем необязательно z₁= z₂. Значит, не всегда существует такой элемент z, что (x, z)ÎR₁и (x, z)ÎR₂, а, следовательно, не будет принадлежности пересечению R₁ и R₂.

Свойство 7в.

Возьмём любую пару (x, y)ÎR₁, что эквивалентно (y, х)ÎR₁^–1. Пусть теперь R₁Í R₂, т.е. из (x, y)ÎR₁следует (x, y)ÎR₂. Перейдя к обратным отношениям, получим, что из (y, х)ÎR₁^–1 вытекает (y, х)ÎR₂^–1, что и означает требуемое свойство.

Свойство 8а).

Докажем предварительно равенство =.

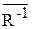Пусть (x, y)Î . Следовательно, (y, x) Î`R или, другими словами, (y, x)ÏR. Отсюда, ( x, y)Ï R^–1, что означает (x, y)Î 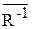. Если же (x, y) Î 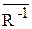, то (x, y) ÏR^–1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R )^–1.

Для доказательства свойства 8а) воспользуемся доказанным равенством и известными свойствами операций над множествами и отношениями.

(R₁È R₂)^d == =

= (`R₁Ç`R₂)^–1 =`R₁^–1 Ç R₂^–1 = R₁^d Ç R₂^d.