Проверка функций на их принадлежность для предсказания значения признака-результата

3.3.1 Линейная функция вида y = ax + b

 

После проверки данной линейной функции имеем следующую картину (Рис.3.)

Рис.3. Модель линейной функции

 

По данному графику видно, что между Х и Y нет функциональной линейной зависимости, т.к. точки разбросаны вокруг графика. Теперь посмотрим на суммарную таблицу значений параметров (Рис.4.)

 

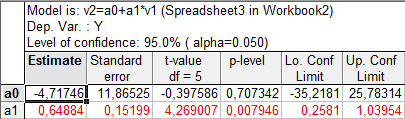
Рис.4. Результаты расчета параметров

 

Первый столбец есть оценка параметров a и b линейной функции. Второй – стандартная ошибка. Третий – статистическая значимость, т.е. насколько можно верить значениям параметров.

В данном случае параметр а – значим, т.к. строка красная, а второй параметр b – незначим. Если хотя бы один параметр незначим, то функция не принимается.

Рис.4. Результаты дисперсионного анализа

Из данной таблицы необходимо взять остаточную дисперсию (пересечение столбца Mean Squares и строки Residual) для расчета границ доверительного интервала.

Далее, необходимо рассчитать доверительный интервал для этой функции, но, т.к. присутствует незначимый параметр, это делать не имеет смысла.

3.3.2. Парабола вида ax^2+bx+c=y

После проверки данной квадратной функции имеем следующую картину (Рис.5.)

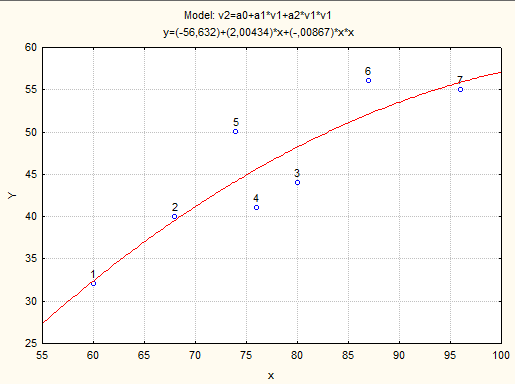
Рис.5. Модель квадратной функции

 

По данному графику видно, что между Х и Y нет функциональной квадратной зависимости, т.к. точки разбросаны вокруг графика. Теперь посмотрим на суммарную таблицу значений параметров (Рис.6.).

Рис.6. Результаты расчета параметров

Первый столбец есть оценка параметров a и b линейной функции. Второй – стандартная ошибка. Третий – статистическая значимость, т.е. насколько можно верить значениям параметров. В данном случае все параметры незначимы. Следовательно, функция не принимается.

 

Рис.7. Результаты дисперсионного анализа

Из данной таблицы необходимо взять остаточную дисперсию (пересечение столбца Mean Squares и строки Residual) для расчета границ доверительного интервала. К сожалению, все параметры незначимые и интервал не рассчитывается.

3.3.3. Функция вида ax^b=y

 

После проверки данной квадратной функции имеем следующую картину (Рис.8.)

Рис.8. Модель степенной функции

 

По данному графику видно, что между х и Y нет функциональной степенной зависимости, т.к. точки разбросаны вокруг графика. Теперь посмотрим на суммарную таблицу значений параметров (Рис.6.).

Рис.9. Результаты расчета параметров

Первый столбец есть оценка параметров a и b линейной функции. Второй – стандартная ошибка. Третий – статистическая значимость, т.е. насколько можно верить значениям параметров. В данном случае параметр а – значим, т.к. строка красная, а второй параметр b – незначим. Если хотя бы один параметр незначим, то функция не принимается.

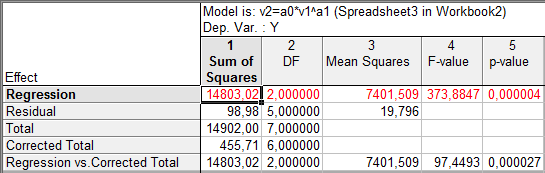
Рис.10. Результаты дисперсионного анализа

Из данной таблицы необходимо взять остаточную дисперсию (пересечение столбца Mean Squares и строки Residual) для расчета границ доверительного интервала. К сожалению, все параметры незначимые и интервал не рассчитывается.