Погрешность произведения приближенных величин

Лекция № 3

Рассмотрим теперь произведение приближенных величин. Пусть

.

Тогда

,

.

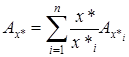Таким образом, при умножении приближенных величин отно­сительные погрешности складываются.

Оценим грубо число вер­ных знаков в произведении m множителей, заданных в десятичной системе счисления, имеющих одинаковое число k верных знаков, если . Обозначим через пер­вые цифры сомножителей, отличные от нуля. Эти цифры называют первыми значащими цифрами. Тогда по данной ранее приближенной формуле

.

Отсюда

.

Обозначив через b первую значащую цифру произведения, будем иметь:

.

Заменим в правой части b на 9 и на 1. Получим:

.

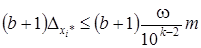Так как , то

.

Таким образом, будем иметь, по крайней мере, верных знаков. Оценка очень груба, и практически мы будем иметь 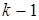верных знаков, а иногда и k.

При умножении вручную двух сомножителей с целью экономии времени и сокращения записей более точный сомножитель округляют так, чтобы число его верных знаков было на 1 больше, чем у менее точного.