Косвенные способы измерения расстояний

Рисунок 24 - Схема измерения линии на наклонном участке

Рисунок 23 - Принцип измерения расстояния оптическим дальномером

Для измерения линии на одном конце устанавливают прибор, а на другом рейку.

Пусть визирная ось трубы горизонтальна. Из подобия треугольников

AFB и a'Fb' следует, что OF/AB=OF/a'b'. Введём обозначения: AB=n; 0F=D'; FO=f; a'b'=P, то:

D'/n=f/n,откуда D'=f/P ^. n,

где f – фокусное расстояние объектива;

P – расстояние между дальномерными нитями;

n – расстояние между нитями по рейке;

D' – расстояние от рейки до переднего фокуса объектива F.

Отношение f/P для данного прибора величина постоянная и называется коэффициентом дальномера, её обозначают буквой "К", то есть f/P=K. Поэтому:

D' = K ^. n (14)

На рисунке видно, что для получения расстояния от оси прибора до рейки необходимо прибавить фокусное расстояние f и расстояние от объектива до оси вращения трубы δ.

Таким образом: d = D + f + δ.

Расстояние f + δ обозначают C =f + δ и называют постоянным слагаемым дальномера. Для определения искомого расстояния имеем:

D = K ^. n + C (15)

В современных приборах постоянное слагаемое мало и его часто не учитывают, тогда предыдущая формула имеет вид:

D = K ^. n (16)

Это рабочая формула дальномера и так как К = 100, то упрощается вычисление. Полученная формула верна для случая, когда рейка расположена перпендикулярно к визирной оси трубы. При измерениях на местности это условие нарушается, так как при наклонном положении визирной оси рейку устанавливают вертикально (рисунок 24).

Если рейка наклонена по отношении к визирной оси на угол v, то вместо правильного отсчёта M'N'=m возьмут отсчёт MN=n. Эти величины связаны соотношением n'=n ^. cos v, но так как d=D ^. cos v, то:

d = K ^. n ^. cos v. (17)

 

 

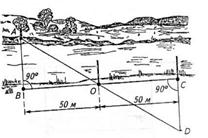
На практике встречаются случаи, когда для измерения линий невозможно использовать ленту из-за препятствий (река, болото, овраг, лес и т.д.). Наиболее часто встречающийся случай определения недоступного расстояния показан на рисунке 25 а.

а) б)

в) г)