Информация, сообщения, сигналы
Сообщения и сигналы
В разделе №2 рассмотрены сведения, позволяющие составить представление о главном объекте деятельности предприятий связи: информация, сообщение, сигнал. Приведены виды сигналов (дискретные, непрерывные), их параметры (спектр, полоса пропускания сигнала).
Особое внимание уделено процессу формирования электрического сигнала в зависимости от вида источника сообщения (речевое сообщение, электронно-лучевая трубка, факсимильный сигнал, телеграфия). Дана методика определения основных параметров этих сигналов, позволяющая определить мощность сигнала (среднюю, пиковую), а также пик-фактор сигнала и его динамический диапазон.
Информация – это сведения, являющиеся объектом передачи, распределения, преобразования, хранения или непосредственного использования. Сообщение является формой представления информации.
Количество информации в отдельно взятом сообщении определяется величиной, обратной вероятности появления сообщения, вычисленной в логарифмических единицах:
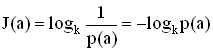 , (2.1)
, (2.1)
где р(а) – вероятность сообщения а,
k – основание логарифма.
При р(а)=1 количество информации равно нулю, то есть сообщение об известном событии никакой информации не несет.
Основание логарифма чаще всего принимают равным двум (k=2), и тогда количество информации, содержащейся в сообщении, выражается в двоичных единицах:
 , (2.2)
, (2.2)
Двоичную единицу обычно называют битом – от binary digit (двоичная цифра).
Совокупность всех возможных сообщений и вероятностей их появления образует ансамбль сообщений. Если ансамбль состоит всего из двух сообщений а1 и а2 (например, вида "да" и "нет" или 0 и 1), которые являются независимыми и равновероятными, то есть р(а1)= р(а2) = 1/2, то каждое из сообщений несет одну двоичную единицу (один бит) информации:
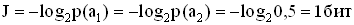 , (2.3)
, (2.3)

Рисунок 2.1 – Принцип передачи сообщений
Различают четыре вида сигналов: непрерывный сигнал непрерывного времени (рисунок 2.2, а), непрерывный дискретного времени (рисунок 2.2, б), дискретный непрерывного времени (рисунок 2.2, в) и дискретный дискретного времени (рисунок 2.2, г) [27].

Рисунок 2.2 – Непрерывный сигнал непрерывного времени (а), непрерывный сигнал дискретного времени (б), дискретный сигнал непрерывного времени (в), дискретный сигнал дискретного времени (г).
Все сигналы могут быть подразделены на периодические, значения которых повторяются через определённые промежутки времени, и непериодические. Простейшим периодическим сигналом является гармоническое колебание [1].
S(t)=A∙Sin(ω∙t), (2.4)
где A, ω – амплитуда и угловая частота колебания.
Любой периодический сигнал состоит из гармоник. Значение амплитуд (Аk),частот (ωk) и начальных фаз (φk) которых можно найти, посредством разложения в ряд Фурье:
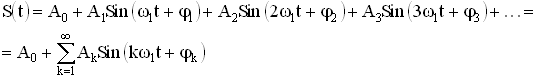
Формула (2.5)
Если изобразить амплитуду Аk и фазу φk каждой гармоники на рисунке, то получим спектральные диаграммы. Распределение амплитуд Аk гармоник по частоте называется спектром амплитуд сигнала, а распределение фаз φk – спектром фаз. На рисунке 2.3 изображены временное и спектральное представления электрических сигналов [1].
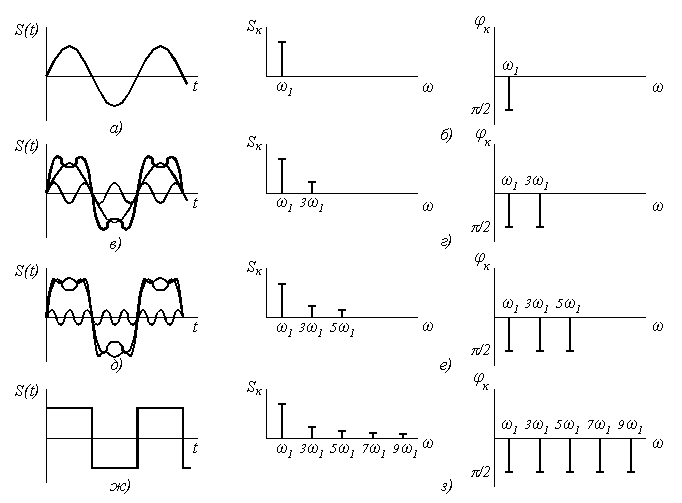
Рисунок 2.3 – Временное и спектральное представления электрических сигналов
Непериодический сигнал легко получить из периодического, увеличивая период вплоть до бесконечности (на рисунке 2.4 показано последовательное двукратное увеличение периода). Спектральные диаграммы, соответствующие каждому периоду приведены на рисунке 2.5.
 Рисунок 2.4 – Увеличение периода последовательности прямоугольных импульсов Рисунок 2.4 – Увеличение периода последовательности прямоугольных импульсов
|  Рисунок 2.5 – Переход к спектральной плотности одиночного прямоугольного импульса Рисунок 2.5 – Переход к спектральной плотности одиночного прямоугольного импульса
|
При увеличении периода сигнала частота первой гармоники понижается и спектральные линии становятся гуще. Амплитуды гармоник уменьшаются, так как энергия сигнала перераспределяется между возросшим числом гармоник. Понятие спектра амплитуд заменяется понятием спектральной плотности амплитуд (аналогично возникает понятие спектральной плотности фаз), которая указывает на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот (рисунок 2.5). Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.