Надежность, как один из основных показателей качества программы
Надежность программы заключается в ее правильности. Правильность алгоритмов и программ очень важна, т.к. мы хотим знать всегда ли они будут давать требуемые результаты. Бессмысленно говорить правилен ли алгоритм или нет, если мы не поняли до конца задачу, что этот алгоритм должен решать.
Правильность алгоритмов и программ может обсуждаться тогда, когда имеются четкие определения правильности результатов. Программа является правильной, если она дает правильные результаты при допустимых исходных данных.
В качестве примера рассмотрим алгоритм вычисления 10-й степени числа, а затем докажем его правильность.
Начало вещ. х; у;
Ввод (х)
у: = х*х; (у1*х);
у: = у*у; (у2 = у1*у1);
у: = у*х; (у3 = у2*х);
у: = у*у; ( у = у3*у3)
вывод (у)
конец
Утверждение: при любом аргументе х конечное значение, вычисляемое данным алгоритмом будет равно у = х10.
Доказательство: рассмотрим промежуточные результаты вычислений, выписанные справа.
Проведем подстановки.
у=у3*у3=у32=у2х=(у2х)2=(у1*у1*х)2=(у12*х)2=3((х*х)2*х)2=(х4*х)2=х10
Ценность доказательств в правильности состоит в том, что они могут вскрыть ошибки в алгоритмах. Наличие ошибок означает, что можно указать такие допустимые данные, при которых выполнение алгоритма дает неправильные результаты либо вообще никаких результатов.
Рассмотрим вариант программы, вычисляющей максимальное из 3-х чисел.
Начало вещ а, b, с, max;
Ввод (а, b, с);
Если а ≥ b, то max:= b;
Иначе max ≥ c;
Вывод (max);
Конец
Утверждение: конечный результат выполнения приведенного алгоритма (значение max при любых значениях а, b, с есть max из этих 3-х значений).
Доказательство: для алгоритмов, содержащих выбор действий, анализ требует разбора всех случаев. В данном примере возможны три основные ситуации:
1. конечный результат равен первому числу (max:= а).
2. результат равен двойному числу (max:= b).
3. результат равен тройному числу (max:= с).
Разберем 1-ю ситуацию. В приведенной программе результат max=а будет получен, если а≥ b. При этом не учитывается значение переменной с, которая может оказаться больше а, следовательно, алгоритм неправильный, и это можно подтвердить на примере а=2, b=1, с-3. Т.е. одной проверки а≥ b недостаточно, необходимо проверять еще и условие а≥с.
Выводы:
1. для утверждения о наличии ошибок в алгоритме достаточно указать контрпример. Контрпример – это набор допустимых данных, при котором будет получен неправильный результат, либо результатов не будет получено совсем.
2. для утверждения об отсутствии ошибок в алгоритме необходимо доказать, что правильные результаты будут получены при любых допустимых исходных данных. А для этого необходим исчерпывающий анализ правильности результатов при любых допустимых исходных данных.
Пример оценки качества программы
Оценить качество программы, решающей следующую задачу:
Решить квадратное уравнение:
ax2 + bx = c = 0 для общего случая. Комплексное решение представить в виде значений модуля и аргумента комплексно сопряженных корней. Представив общую формулу решения
X1,2 =  в виде
в виде
P = 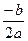 q =
q =  мы затем в зависимости от знака D = b2 – 4ac найдем для вещественного случая
мы затем в зависимости от знака D = b2 – 4ac найдем для вещественного случая
Кор1= р + q
Кор2= p – q, а для комплексного
Кор1= 

Кор2= arcsin 
В результате введя до экономии вычислений еще несколько промежуточных величин, получим следующую программу:
Начало вещ. a, b, c, r, d, p, q, кор1, кор2;
Цел. Pr;
Ввод (a, b, c);
D:=b**2-4ac*c;
P:=-b/2*a;
Q:=sqrt (d)/2*a;
Если d < 0 то
Начало r:=p**2+a**2;
кор1:=sqrt (r);
кор2:= arcsin(q/ кор1);
Конец
Иначе
Начало кор1:=p+q;
кор2:=p-q;
Конец
Pr:=sign(d);
Вывод (pr, кор1, кор2);
Конец
Требуется оценить качество приведенной программы.