Элементы комбинаторики
Классическое определение вероятности событий
Определение 1.9.Вероятность события 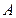 – количественная мера неопределенности, число, которое выражает степень уверенности в наступлении этого события.
– количественная мера неопределенности, число, которое выражает степень уверенности в наступлении этого события.
Проведем следующее испытание. Бросим один игральный кубик. В результате такого испытания возможны такие события: «выпала единица», «двойка», «тройка», «четверка», «пятерка» и «шестерка». Эти события, очевидно, образуют полную группу. Изобразим их совокупность в виде отдельных точек на плоскости (см. рис. 1.1). Введем следующие определения. Единичный, отдельный исход испытания называется элементарным событием (элементарным исходом). Набор всех элементарных событий – множество элементарных исходов (пространство элементарных событий 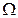 ). Таким образом, любое событие можно рассматривать как подмножество пространства элементарных событий. Мы говорим, что событие произошло, если в результате испытания произошло элементарное событие, принадлежащее этому подмножеству. Например, нас интересует событие
). Таким образом, любое событие можно рассматривать как подмножество пространства элементарных событий. Мы говорим, что событие произошло, если в результате испытания произошло элементарное событие, принадлежащее этому подмножеству. Например, нас интересует событие 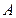 – выпало четное число. Этому событию соответствует набор (подмножество) трех элементарных событий – «двойка», «четверка» и «шестерка». Появление одного из этих элементарных событий будет означать, что произошло интересующее нас событие
– выпало четное число. Этому событию соответствует набор (подмножество) трех элементарных событий – «двойка», «четверка» и «шестерка». Появление одного из этих элементарных событий будет означать, что произошло интересующее нас событие 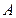 . Как в данном случае можно определить вероятность события? Очевидно, что чем выше удельный вес элементарных событий, соответствующих интересующему нас событию, тем больше шансов, что оно появится, т.е. тем выше вероятность. В нашем случае всего 6 элементарных исходов, из них 3 четных числа. Таким образом, вероятность будет равна
. Как в данном случае можно определить вероятность события? Очевидно, что чем выше удельный вес элементарных событий, соответствующих интересующему нас событию, тем больше шансов, что оно появится, т.е. тем выше вероятность. В нашем случае всего 6 элементарных исходов, из них 3 четных числа. Таким образом, вероятность будет равна 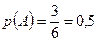 .
.
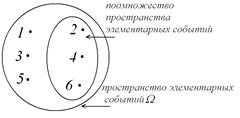
Рис. 1.1.
Рассмотренный метод является классическим, и сформировался в XVII веке в результате анализа азартных игр, и основан на понятии равновозможности событий.
Определение 1.10. Вероятностью наступления события 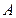 называется отношение числа всех благоприятствующему этому событию элементарных исходов
называется отношение числа всех благоприятствующему этому событию элементарных исходов 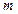 к общему числу всевозможных простых, попарно несовместных, единственно возможных и равновозможных элементарных исходов испытания
к общему числу всевозможных простых, попарно несовместных, единственно возможных и равновозможных элементарных исходов испытания  :
:
 (1.1)
(1.1)
Число элементарных исходов, благоприятствующих данному событию, принадлежит, очевидно, следующему отрезку: 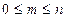 . Разделив данное неравенство на
. Разделив данное неравенство на  , получим
, получим 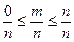 . Отсюда следует, что диапазон изменения вероятности случайного события:
. Отсюда следует, что диапазон изменения вероятности случайного события: 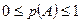 . Вероятность достоверного события:
. Вероятность достоверного события:  . Вероятность невозможного события:
. Вероятность невозможного события: 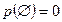 . Чем больше значение вероятности, тем более мы уверены в наступлении события. Приведем несколько примеров на нахождение вероятности наступления событий с использованием классического определения вероятности.
. Чем больше значение вероятности, тем более мы уверены в наступлении события. Приведем несколько примеров на нахождение вероятности наступления событий с использованием классического определения вероятности.
Пример 1.7. В урне 4 красных и 8 зеленых яблока. Случайным образом вынули одно яблоко. Найти вероятность того, что это яблоко – зеленое.
Решение:
Пусть событие 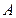 заключается в появлении зеленого яблока. В данной задаче число всевозможных исходов
заключается в появлении зеленого яблока. В данной задаче число всевозможных исходов 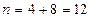 , число исходов, которые благоприятствуют наступлению события
, число исходов, которые благоприятствуют наступлению события 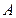
 . Тогда, согласно классическому определению вероятности:
. Тогда, согласно классическому определению вероятности:
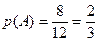 .
.
Пример 1.8. Одновременно бросили два игральных кубика. Какова вероятность того, что на обеих гранях выпадет в сумме 8 очков?
Решение:
Пусть событие 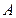 заключается в том, что при одновременном бросании двух кубиков выпадет число 8. Число всех возможных исходов
заключается в том, что при одновременном бросании двух кубиков выпадет число 8. Число всех возможных исходов 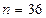 , поскольку каждому значению на одном кубике может соответствовать 6 значений на другом
, поскольку каждому значению на одном кубике может соответствовать 6 значений на другом 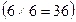 . Для благоприятных исходов составим следующую таблицу:
. Для благоприятных исходов составим следующую таблицу:
| Кубик №1 | |||||
| Кубик №2 |
Получили всего благоприятных исходов  . Вычисляем вероятность:
. Вычисляем вероятность:
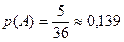 .
.
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. они в ряде случаев позволяют подсчитать количество всевозможных и количество благоприятных исходов.
Правило умножения в комбинаторике. Если первое действие можно осуществить 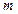 различными способами, а второе –
различными способами, а второе –  , то оба действия можно осуществить
, то оба действия можно осуществить 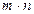 различными способами.
различными способами.
Это правило обобщается и на большее число действий. Если элемент 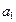 можно выбрать
можно выбрать 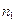 способами, после каждого выбора этого элемента следующий за ним элемент
способами, после каждого выбора этого элемента следующий за ним элемент 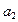 можно выбрать
можно выбрать 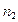 способами, ..., после выбора элементов
способами, ..., после выбора элементов 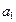 ,
, 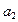 , ...,
, ...,  , элемент
, элемент 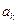 выбирается
выбирается 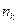 способами, то все
способами, то все 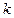 элементов
элементов 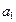 ,
, 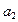 , ...,
, ..., 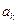 можно выбрать
можно выбрать  способами.
способами.
Пример 1.9. Сколько слов, содержащих 6 букв, можно составить из 33 букв русского алфавита при условии, что любые две стоящие рядом буквы различны (например, слово «корова» допускается, а слово «колосс» нет)? При этом учитываются не только слова, имеющие смысл, но и такие бессмысленные, как «трнатк» и т. п.
Решение:
В этом случае на первое место у нас 33 кандидата. Но после того как первая буква выбрана, вторую можно выбрать лишь 32 способами – ведь повторять первую букву нельзя. На третье место тоже 32 кандидата – первую букву уже можно употребить, а вторую – нельзя. Так же убеждаемся, что на все места, кроме первого, имеется 32 кандидата. А так как число этих мест равно 5, то получаем ответ 33∙32∙32∙32∙32∙32 = 33∙325 = 1107296256.
Определение 1.11. Факториалом целого положительного числа  (обозначается
(обозначается 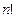 ) называется произведение первых
) называется произведение первых  чисел натурального ряда, т.е.:
чисел натурального ряда, т.е.:
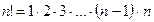 (1.2)
(1.2)
При этом полагают, что 1!=1 и 0!=1. Последнее равенство следует из следующих рассуждений. Факториал обладает очевидным свойством: 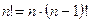 . Это равенство справедливо при
. Это равенство справедливо при 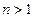 . Естественно определить 0! так, чтобы оно осталось верным и при
. Естественно определить 0! так, чтобы оно осталось верным и при 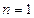 , т.е. так, чтобы 1!=1∙0!. Но тогда нужно положить 0!=1.
, т.е. так, чтобы 1!=1∙0!. Но тогда нужно положить 0!=1.
Пусть имеется некоторое множество из  элементов
элементов 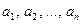 . Из этого множества можно образовать разные выборки, каждая из которых содержит
. Из этого множества можно образовать разные выборки, каждая из которых содержит 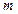 элементов
элементов 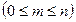 .
.
Определение 1.12. Если комбинации из  элементов по
элементов по 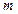 отличаются либо составом элементов, либо порядком их расположения (либо и тем и другим), то такие комбинации называются размещениями из
отличаются либо составом элементов, либо порядком их расположения (либо и тем и другим), то такие комбинации называются размещениями из  элементов по
элементов по 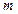 .
.
Доказательство. При составлении  размещений из
размещений из  элементов нам надо сделать
элементов нам надо сделать 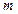 выборов. Сначала можно выбрать любой из имеющихся
выборов. Сначала можно выбрать любой из имеющихся  предметов. Если этот выбор уже сделан, то на втором шаге приходится выбирать из оставшихся
предметов. Если этот выбор уже сделан, то на втором шаге приходится выбирать из оставшихся 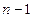 элементов – ведь повторять сделанный выбор нельзя. Точно так же на третьем шаге для выбора остается
элементов – ведь повторять сделанный выбор нельзя. Точно так же на третьем шаге для выбора остается 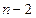 свободных элементов, на четвертом –
свободных элементов, на четвертом –  и т. д. Таким образом, по правило умножения в комбинаторике число размещений из
и т. д. Таким образом, по правило умножения в комбинаторике число размещений из  элементов по
элементов по 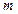 равно:
равно:
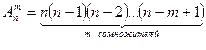 (1.3)
(1.3)
или:
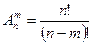 (1.4)
(1.4)
Пример 1.10. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
Решение:
Это есть число размещений:
 .
.
Определение 1.13. Если комбинации из  элементов отличаются только порядком расположения этих элементов, то их называют перестановками из
элементов отличаются только порядком расположения этих элементов, то их называют перестановками из  элементов. Число перестановок из
элементов. Число перестановок из  элементов:
элементов:
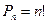 (1.5)
(1.5)
Пример 1.11. Сколькими способами можно разместить 5 человек за столом, на котором поставлено 5 приборов?
Решение:
Это есть количество перестановок:  .
.
Определение 1.14. Если комбинации из  элементов по
элементов по 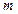 отличаются только составом элементов, то их называют сочетаниями из
отличаются только составом элементов, то их называют сочетаниями из  элементов по
элементов по 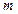 . Число сочетаний из
. Число сочетаний из элементов по
элементов по 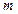 :
:
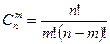 (1.6)
(1.6)
Доказательство. Число размещений 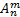 можно найти следующим образом: выбрать
можно найти следующим образом: выбрать 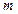 элементов из множества, содержащего
элементов из множества, содержащего  элементов(это можно сделать
элементов(это можно сделать  способами); затем в каждом из полученных сочетаний сделать все возможные перестановки (это можно сделать
способами); затем в каждом из полученных сочетаний сделать все возможные перестановки (это можно сделать 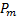 способами). Следовательно, согласно правилу умножения в комбинаторике, можно записать:
способами). Следовательно, согласно правилу умножения в комбинаторике, можно записать: 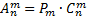 . Отсюда
. Отсюда 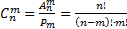 .
.
Свойства сочетаний:
1) 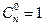 ; 2)
; 2) 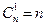 ; 3)
; 3)  ; 4)
; 4) 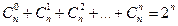 ; 5)
; 5) 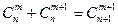 .
.
Пример 1.12. В хоккейном турнире участвуют 6 команд. Сколько матчей должно быть сыграно в турнире, если между любыми двумя командами должен быть сыгран только один матч?
Решение:
Каждый матч играется между двумя командами из 6 и отличаются только составом пар команд, т.е. представляют сочетание из 6 элементов по 2. Таким образом, находим:
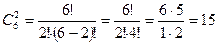 .
.
Пример 1.13. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность, что выбраны два мальчика? Выбор считать случайным.
Решение:
Событие 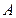 состоит в том, что в члены делегации выбрали двоих мальчиков. Для решения этой задачи воспользуемся классическим определением вероятности, т.е.:
состоит в том, что в члены делегации выбрали двоих мальчиков. Для решения этой задачи воспользуемся классическим определением вероятности, т.е.:  .
.
Число исходов, благоприятствующих наступления события 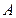 равно:
равно:
 .
.
Число всех возможных исходов  :
: 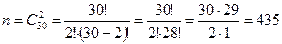 .
.
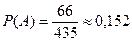 .
.
Определение 1.15.Если выбирать 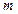 элементов из
элементов из  , возвращая каждый выбранный элемент обратно, то такая выборка называется размещением из
, возвращая каждый выбранный элемент обратно, то такая выборка называется размещением из  по
по 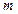 с повторениями.
с повторениями.
При этом 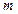 и
и  могут находиться в любом соотношении:
могут находиться в любом соотношении:  и
и  .
.
Общее количество 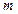 выборок с возвращением равно:
выборок с возвращением равно:
 (1.7)
(1.7)
Пример 1.14. Сколько различных трехзначных чисел можно составить из цифр 1, 2 ,3, 4, 5?
Решение:
Воспользуемся формулой (1.7). В данной задаче  = 5,
= 5, 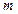 = 3.
= 3.  .
.