Метод максимального правдоподобия

Существует несколько методов получения точечных оценок. Метод, который чаще приводит к наилучшим оценкам, называется метод максимального правдоподобия (предложен Р. Фишером).

Пусть – непрерывная случайная величина, которая в результате испытаний приняла значения . Пусть вид плотности распределения данной случайной величины известен, но не известен параметр , которым определяется эта функция.

Определение 16.4. Функция вида:

называется функцией правдоподобия.

Метод максимального правдоподобия заключается в том, что в качестве оценок параметра принимается то значение , при котором функция принимает максимальное значение. Экстремум функций и достигается при одних и тех же значениях . Удобнее находить максимум функции . Поэтому критические значения определяются из системы уравнений правдоподобия:

где – число оцениваемых параметров.

Данный метод дает состоятельные оценки. Если существует эффективная оценка, то метод максимального правдоподобия дает эту оценку. Оценки максимального правдоподобия асимптотически эффективны и имеют асимптотически нормальное распределение.

Пример 16.1. Найти методом наибольшего правдоподобия оценку параметра λ показательного распределения:

если в результате испытаний случайная величина распределенная по показательному закону, приняла значения .

Решение:

Составим функцию правдоподобия, учитывая, что :

Отсюда следует:

Логарифмическая функция правдоподобия:

Найдем первую производную по переменной λ:

Напишем уравнение правдоподобия, для чего приравняем первую производную нулю:

Отсюда критическая точка равна:

Найдем вторую производную по λ:

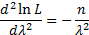
При вторая производная отрицательна, следовательно, является точкой максимума. Значит, в качестве оценки наибольшего правдоподобия параметра показательного распределения надо принять величину, обратную выборочной средней: .