Теорема. Пусть дана система дифференциальных уравнений
ГЛАВА V. Устойчивость
Дифференциальное уравнение или система, описывающие какой-либо физический процесс, обычно таковы, что участвующие в них функции, а также числовые коэффициенты и начальные условия задаются приближённо, с какой-либо степенью точности. Если решение уравнения меняется сильно при незначительном изменении этих данных, то такое решение неустойчиво и появляются серьёзные сомнения в том, что эти функции действительно описывают данный процесс. Естественным требованием поэтому является устойчивостьрешений. Из различных понятий устойчивости мы выберем наиболее употребительное – устойчивость по Ляпунову.
Пусть
 (1)
(1)
– система дифференциальных уравнений, записанная в векторной форме (здесь  неизвестная вектор-функция). Рассматриваются решения этой системы, удовлетворяющие начальному условию
неизвестная вектор-функция). Рассматриваются решения этой системы, удовлетворяющие начальному условию 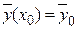 и определённые на полуоси
и определённые на полуоси  Решение
Решение  называется устойчивым по Ляпунову, если для любого
называется устойчивым по Ляпунову, если для любого  найдется такое
найдется такое  , что для всякого решения
, что для всякого решения  , начальные условия которого удовлетворяют неравенствам
, начальные условия которого удовлетворяют неравенствам

для всех  , то справедливы неравенства
, то справедливы неравенства
 .
.
Дадим геометрическую интерпретацию этому определению.

Рис.1.
На рис.1. приведен график i-ой компоненты невозмущенного решения  . В окрестности этой компоненты построен «коридор» шириной
. В окрестности этой компоненты построен «коридор» шириной  . Тогда для любого фиксированного значения
. Тогда для любого фиксированного значения 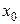 найдется такое
найдется такое  , зависящее от
, зависящее от  , что как только начальные условия компоненты возмущенного решения
, что как только начальные условия компоненты возмущенного решения  окажутся внутри отрезка
окажутся внутри отрезка  , график компоненты
, график компоненты  полностью займет место внутри коридора шириной
полностью займет место внутри коридора шириной  .
.
Если же для заданного  при любом сколь угодно малом
при любом сколь угодно малом  неравенство
неравенство  не выполняется при всех
не выполняется при всех  хотя бы для одного значения
хотя бы для одного значения  , то решение
, то решение 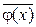 называется неустойчивым.
называется неустойчивым.
Если решение 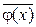 не только устойчиво, но и удовлетворяет условию
не только устойчиво, но и удовлетворяет условию
 . (2)
. (2)
при условии  , то решение называется асимптотически устойчивым.
, то решение называется асимптотически устойчивым.
Если частное решение системы
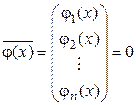 ,
,
то есть, если все  при всех значениях аргумента
при всех значениях аргумента  равны нулю, то такое решение называется точкой покоя.
равны нулю, то такое решение называется точкой покоя.
Исследование устойчивости данного решения 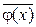 значительно упрощается, если вместо
значительно упрощается, если вместо  ввести вектор
ввести вектор  .
.
Тем самым задача сводится к устойчивости точки покоя  .
.
Не вводя новых обозначений, считаем, что исследуемой на устойчивость функцией будет вектор-функция  .
.
Формулировка устойчивости по Ляпунову для тривиального нулевого решения принимает вид:
Точка покоя системы устойчива по Ляпунову, если  что из неравенства
что из неравенства  следует
следует  для всех
для всех  .
.
Рассмотрим простейшие точки покоя при  для линейных систем
для линейных систем  с
с  :
:
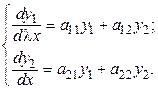
Для этого исследуем общее решение системы. Характеристическое уравнение имеет вид
 (3)
(3)
или сокращенно  где
где 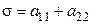 след матрицы
след матрицы 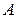 , а
, а 
Рассмотрим частные случаи.
1. Корни характеристического уравнения (3) – действительные различные числа 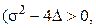 где
где 
Поиск общего решения производится в форме

Коэффициенты 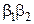 и
и  с точностью до постоянного множителя определяются из однородной системы уравнений
с точностью до постоянного множителя определяются из однородной системы уравнений

При этом возможны следующие варианты.
1а) Если  то точка покоя
то точка покоя  асимптотически устойчива. Устойчивость следует из того, что в какой бы
асимптотически устойчива. Устойчивость следует из того, что в какой бы  -окрестности точка не находилась, с течением времени
-окрестности точка не находилась, с течением времени  интегральная кривая остается внутри куба
интегральная кривая остается внутри куба  так как
так как  монотонно стремится к нулю. Поэтому
монотонно стремится к нулю. Поэтому  можно положить равным
можно положить равным  . Система асимптотически устойчива, так как
. Система асимптотически устойчива, так как  Точка покоя в этом случае называется устойчивым узлом (см.рис.2).
Точка покоя в этом случае называется устойчивым узлом (см.рис.2).

Рис.2.
1б)  . Точка покоя здесь называется неустойчивым узлом. Форма интегральных кривых такая же , как в предыдущем случае, но стрелки направлены противоположно. Из любого куба со стороны
. Точка покоя здесь называется неустойчивым узлом. Форма интегральных кривых такая же , как в предыдущем случае, но стрелки направлены противоположно. Из любого куба со стороны  (в нашем случаи из квадрата) с увеличением
(в нашем случаи из квадрата) с увеличением  происходитудаление от точки покоя (рис.3).
происходитудаление от точки покоя (рис.3).

Рис.3.
1в) Если корни характеристического уравнения разных знаков (пусть  ), то точка покоя называется седлом. Это неустойчивая точка покоя. Только по одной прямой, когда
), то точка покоя называется седлом. Это неустойчивая точка покоя. Только по одной прямой, когда  а
а  и
и  отличны от нуля, движение по интегральной прямой с увеличением
отличны от нуля, движение по интегральной прямой с увеличением  стремятся к нулю. Но при любом
стремятся к нулю. Но при любом  нельзя найти такую окрестность точки покоя, чтобы все интегральные кривые оставались внутри
нельзя найти такую окрестность точки покоя, чтобы все интегральные кривые оставались внутри  - квадрата (рис.4).
- квадрата (рис.4).

Рис.4.
2. Корни характеристического уравнения комплексные: 
Общее решение системы имеет вид
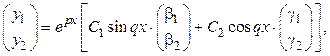
где  - некоторые действительные числа.
- некоторые действительные числа.
Рассмотрим частные случаи.
2а)  . Общий множитель в формуле
. Общий множитель в формуле  стремится к нулю, а
стремится к нулю, а  и
и  остаются ограниченными. Интегральные линии асимптотически приближаются к нулю при
остаются ограниченными. Интегральные линии асимптотически приближаются к нулю при  . Точка покоя называется устойчивым фокусом.
. Точка покоя называется устойчивым фокусом.

Рис.5.
2б)  . Кривые имеют тот же вид, что и в случае 2а), однако с увеличением
. Кривые имеют тот же вид, что и в случае 2а), однако с увеличением  множитель
множитель  неограниченно возрастает, стрелки спирали направлены в сторону удаления от точки покоя, которая называется неустойчивым фокусом (рис.6).
неограниченно возрастает, стрелки спирали направлены в сторону удаления от точки покоя, которая называется неустойчивым фокусом (рис.6).

Рис.6.
2в) Корни чисто мнимые:  . Общее решение имеет вид
. Общее решение имеет вид

Это граничная ситуация между рассмотренными случаями 2а) и 2б). Интегральные кривые являются подобными эллипсами, в общем случае вложенными друг в друга замкнутыми кривыми. Точка покоя называется центром. Это устойчивая точка покоя, так как  можно найти квадрат
можно найти квадрат  такой, что все интегральные кривые будут целиком содержаться в квадрате
такой, что все интегральные кривые будут целиком содержаться в квадрате 
 . Но это не асимптотическая точка покоя, так как никакого стремления к нулю при
. Но это не асимптотическая точка покоя, так как никакого стремления к нулю при  нет.
нет.
3. Если корни кратные и действительные:  , то частные случаи будут следующие.
, то частные случаи будут следующие.
3а) 


Это асимптотически устойчивый узел (рис.7).

Рис.7.
Данный узел занимает промежуточное положение между узлом вида 1а) и устойчивом фокусом, когда появляется мнимая составляющая.
3б)  . Как и в предыдущем случае - узел, но неустойчивый. Движение происходит в направлении от точки покоя. Все интегральные кривые касаются в точке покоя (рис.8).
. Как и в предыдущем случае - узел, но неустойчивый. Движение происходит в направлении от точки покоя. Все интегральные кривые касаются в точке покоя (рис.8).

Рис.8.
4. Если  то общее решение имеет вид
то общее решение имеет вид 
 .
.
Если из двух уравнений  и
и  исключить
исключить  то получим семейство параллельных прямых:
то получим семейство параллельных прямых:
 .
.
4а) Если  имеем устойчивую неасимптотическую точку покоя.
имеем устойчивую неасимптотическую точку покоя.

Рис.9.
4б) Если  неустойчивая точка покоя.
неустойчивая точка покоя.

Рис.10.
Классификация точек покоя при  носит более сложный характер.
носит более сложный характер.
Например, пусть при решении кубического характеристического уравнения один из корней отрицателен и два других комплексно сопряжены с отрицательной действительной частью. Тогда интегральные кривые в окрестности точка покоя носят характер винтообразной спирали, направленной к точке покоя.
Устойчивость нулевого решения неоднородной системы  дифференциальных уравнений с постоянными коэффициентами дается следующей теоремой.
дифференциальных уравнений с постоянными коэффициентами дается следующей теоремой.

где 
 матрица размера
матрица размера  с элементами
с элементами 
 непрерывная вектор-функция, определённая для
непрерывная вектор-функция, определённая для  Пусть
Пусть  – собственные значения матрицы А. Тогда:
– собственные значения матрицы А. Тогда:
(1) если  то всякое решение системы устойчиво;
то всякое решение системы устойчиво;
(2) если  для какого-либо
для какого-либо  то всякое решение системы неустойчиво.
то всякое решение системы неустойчиво.
Теорема не даёт ответа на вопрос об устойчивости решений в случае, когда  при всех
при всех  и
и  для какого-либо
для какого-либо 
Нелинейные системы часто удаётся исследовать на устойчивость, осуществив линеаризацию системы, т.е. замену нелинейной на близкую к ней (в определённом смысле) линейную систему. А именно, пусть система имеет вид
 (
(
Выделим каким-либо способом у функций  главную линейную часть (т.е. разложим функции
главную линейную часть (т.е. разложим функции  по формуле Тейлора до членов первого порядка):
по формуле Тейлора до членов первого порядка):

где  а
а  достаточно мала. Тогда вопрос об устойчивости нелинейной системы сведётся к аналогичному вопросу для линейной системы с постоянными коэффициентами, а он рассматривался в предыдущей теореме. Точный математический смысл высказанного утверждения даётся следующей теоремой, доказательство которой здесь не приводится и может быть найдено в учебниках по дифференциальным уравнениям с более подробным изложением.
достаточно мала. Тогда вопрос об устойчивости нелинейной системы сведётся к аналогичному вопросу для линейной системы с постоянными коэффициентами, а он рассматривался в предыдущей теореме. Точный математический смысл высказанного утверждения даётся следующей теоремой, доказательство которой здесь не приводится и может быть найдено в учебниках по дифференциальным уравнениям с более подробным изложением.