Матрица инцидентности ориентированного графа.

Свойства матрицы инцидентности неориентированного графа.

· Число единиц в i-й строке равно степени i-ой вершины, i = 1, 2, … , р.

· Число единиц в 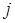-м столбце равно двум, так как любое ребро инцидентно двум вершинам, 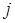= 1, 2, …, р.

· Число единиц в матрице равно удвоенному числу ребер графа.

Если в орграфе G р вершин и q дуг, то элементы его матрицы инцидентности определяются правилом

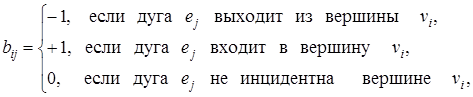
i = 1, …, p; j = 1, … , q.

Пример орграфа и его матрицы инцидентности показан на рис. 12.

 

 

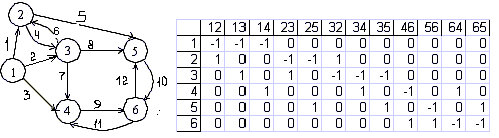
Рис. 12