Расстояние от точки до прямой.
Угол между прямой и плоскостью.


Угол между прямой и плоскостью можно найти через угол между направляющим вектором прямой  и нормальным вектором плоскости
и нормальным вектором плоскости 








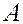
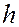



Расстояние от точки 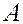 до прямой
до прямой  совпадает с высотой параллелограмма, построенного на векторах
совпадает с высотой параллелограмма, построенного на векторах  и
и  .
.  .
.


ПРИМЕР. Найти расстояние от точки  до прямой
до прямой

РЕШЕНИЕ. 
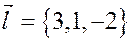

Найдем векторное произведение




Задача 1. Прямая  является пересечением двух плоскостей
является пересечением двух плоскостей  и
и  , заданных уравнениями
, заданных уравнениями  и
и 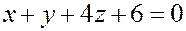 . Написать каноническое уравнение прямой
. Написать каноническое уравнение прямой  .
.
РЕШЕНИЕ. Выпишем решение вырожденной системы
уравнений 
в параметрической форме. Применим метод последовательных исключений Гаусса.
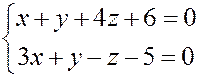 Û
Û 
Обозначая 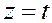 , получим
, получим
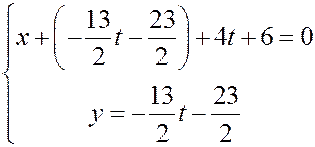
И окончательно

Эту систему уравнений можно интерпретировать как параметрическое уравнение прямой  . Тогда точка, через которую проходит прямая – эта точка
. Тогда точка, через которую проходит прямая – эта точка  (отвечает значению
(отвечает значению  ), а координатами направляющего вектора прямой являются коэффициенты при
), а координатами направляющего вектора прямой являются коэффициенты при  в каждом из трех уравнений системы, то есть
в каждом из трех уравнений системы, то есть  . Таким образом, каноническое уравнение прямой
. Таким образом, каноническое уравнение прямой  имеет вид
имеет вид
 .
.
Задача 2. Даны плоскость  и точка
и точка  . Найти точку
. Найти точку  , симметричную
, симметричную 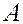 относительно плоскости
относительно плоскости  .
.
РЕШЕНИЕ. Точка  находится на прямой, проходящей через
находится на прямой, проходящей через 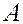 перпендикулярно к плоскости
перпендикулярно к плоскости  , причем
, причем  лежит по другую сторону от плоскости
лежит по другую сторону от плоскости  и на том же расстоянии, что и
и на том же расстоянии, что и 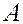 . Другими словами, точка
. Другими словами, точка  - середина отрезка
- середина отрезка 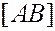 , принадлежит плоскости
, принадлежит плоскости  . Уравнение прямой
. Уравнение прямой  имеет вид
имеет вид 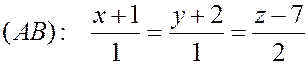
Если координаты точки  обозначить как
обозначить как  , то координаты точки
, то координаты точки  можно найти по формуле деления отрезка в данном отношении:
можно найти по формуле деления отрезка в данном отношении:
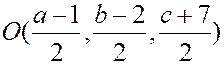 .
.
Следовательно, координаты  точки
точки  удовлетворяют системе уравнений
удовлетворяют системе уравнений

Положим  ,
,
тогда  .
.
Подставляя эти выражения во второе уравнение системы, получим

Умножив на 2, раскрыв скобки и приведя подобные слагаемые, получим
 Û
Û  .
.
Следовательно,
 .
.
Ответ:  .
.
Задача 3. Дана точка  прямая
прямая
 ,
,
и прямая
 .
.
Найти уравнение прямой  , проходящей через точку
, проходящей через точку 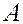 перпендикулярно к прямой
перпендикулярно к прямой  и пересекающей прямую
и пересекающей прямую  .
.
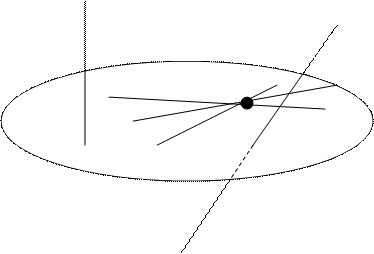
РЕШЕНИЕ. Имеется целая плоскость  , целиком заполненная прямыми, проходящими через точку
, целиком заполненная прямыми, проходящими через точку 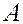 и перпендикулярными к прямой
и перпендикулярными к прямой  . Чтобы найти в ней нужную нам прямую, достаточно найти пересечение плоскости
. Чтобы найти в ней нужную нам прямую, достаточно найти пересечение плоскости  и прямой
и прямой  .
.



Уравнение плоскости  имеет вид:
имеет вид:
 Û
Û  .
.
Пересечение плоскости  и прямой
и прямой  определяется из системы уравнений:
определяется из системы уравнений:

Из последнего уравнения получаем:

Подставляя эти соотношения в первое уравнение системы, получим:
 Û
Û 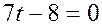 .
.
Следовательно,  и координаты точки
и координаты точки  имеют вид
имеют вид

Направляющий вектор искомой прямой есть
 .
.
Каноническое уравнение прямой имеет вид
 .
.
Лекция 8
Математический анализ
Предел функции одного вещественного
переменного  .
.
Как вычислить значение функции  при
при  , при
, при 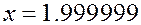 , при
, при 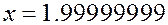 ? Непосредственное вычисление громоздко и, возможно, даст большую погрешность при округлении. Однако, можно попробовать найти
? Непосредственное вычисление громоздко и, возможно, даст большую погрешность при округлении. Однако, можно попробовать найти  , и затем оценить, насколько сильно
, и затем оценить, насколько сильно 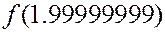 уклоняется от
уклоняется от  . Если уклонение тем меньше, чем меньше разность
. Если уклонение тем меньше, чем меньше разность  , то естественно считать, что
, то естественно считать, что  , а “в пределе” при
, а “в пределе” при  значение
значение  точно равно
точно равно  .
.
Действительно,
 .
.
Таким образом, значения функции  в точках, мало отличающихся от 2, мало отличается от 4. Можно сказать, что 4 есть предел функции
в точках, мало отличающихся от 2, мало отличается от 4. Можно сказать, что 4 есть предел функции  при
при  .
.
Определение. Число 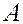 называется пределом функции
называется пределом функции  в точке
в точке  и обозначается как
и обозначается как

если для любого  найдется такое число
найдется такое число  , что
, что  при всех
при всех  .
.
Свойства пределов.
1.  .
.
2. 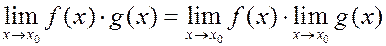 .
.
3. Если  , то
, то  .
.
Лемма о двух милиционерах.
Если 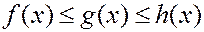 и
и 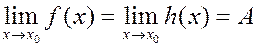 , то
, то  .
.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если  .
.
Теорема. Если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция 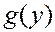 непрерывна в точке
непрерывна в точке  , то композиция
, то композиция  непрерывна в точке
непрерывна в точке  и
и  .
.
Попробуем вычислить  при
при  . Подставим значение
. Подставим значение  в качестве аргумента функции
в качестве аргумента функции  . Получим
. Получим  - “неопределенное” выражение. Какое число в этом случае определяет приближенное значение функции
- “неопределенное” выражение. Какое число в этом случае определяет приближенное значение функции  ? Чтобы это определить, следует “разрешить особенность” функции
? Чтобы это определить, следует “разрешить особенность” функции  в точке
в точке  , иными словами, определить, за счет чего числитель и знаменатель дроби
, иными словами, определить, за счет чего числитель и знаменатель дроби  обращаются в ноль при подстановке 1 вместо
обращаются в ноль при подстановке 1 вместо  . Имеем:
. Имеем:
 .
.
Следовательно,
 .
.
Пример.

Вновь непосредственный подсчет приводит к неопределенности:
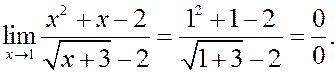
Числитель можно разложить на множители
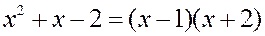 ,
,
Преобразуем знаменатель, домножив и числитель, и знаменатель дроби на сопряженное выражение - сумму 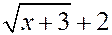 :
:

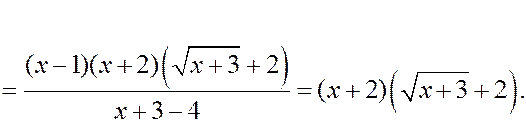
Теперь

Первый замечательный предел.
Рассмотрим предел 
Прямое вычисление дает:

 Для вычисления предела воспользуемся леммой о двух милиционерах.
Для вычисления предела воспользуемся леммой о двух милиционерах.



 1
1 




 1
1

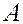
Напишем неравенство для площадей треугольника  , углового сектора
, углового сектора  и треугольника
и треугольника  :
:

 .
.
Поделим все на  (поскольку функция
(поскольку функция 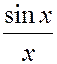 четная, то можно считать, что
четная, то можно считать, что  ):
):
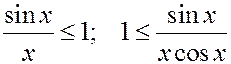 ,
,
откуда
 .
.
Следовательно,
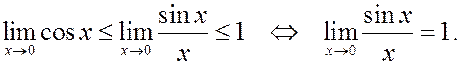
Полученная формула называется первым замечательным пределом.
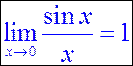
Пример. Вычислить предел
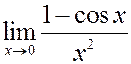
Решение.

Окончательно,

Предел функции на бесконечности.
Определение. Число 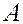 называется пределом функции
называется пределом функции  при
при  , если для любого
, если для любого  найдется такое число
найдется такое число  , что
, что  при всех
при всех  .
.
Обозначается этот предел как

Если в определении предела считать, что  или
или 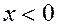 , то получится определение одностороннего предела
, то получится определение одностороннего предела  или
или  соответственно.
соответственно.
Очевидные пределы
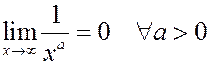

Пример. Вычислить предел
 .
.
Решение. Разделим и числитель и знаменатель на старшую степень  . Имеем:
. Имеем:
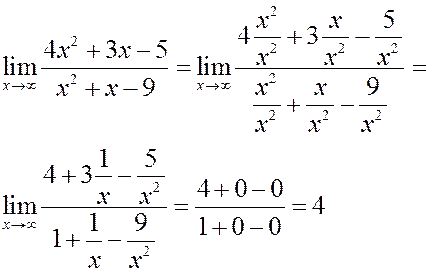
Пример. Вычислить предел 
Решение.

При  получаем
получаем

При  получаем
получаем

Второй замечательный предел.
Теорема (без доказательства). Предел  монотонно возрастающей ограниченной функции (то есть
монотонно возрастающей ограниченной функции (то есть  и
и  для произвольных
для произвольных  ) существует и удовлетворяет неравенству
) существует и удовлетворяет неравенству  .
.
 .
.
Доказательство существования. Рассмотрим сначала функцию 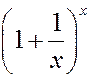 при натуральных значениях аргумента
при натуральных значениях аргумента  .
.
Покажем, что функция  монотонно возрастает. Воспользуемся формулой бинома Ньютона
монотонно возрастает. Воспользуемся формулой бинома Ньютона
 где
где

(в числителе столько же множителей, сколько их имеется в знаменателе). Всего в формуле бинома  слагаемых. Доказывается формула бинома индукцией по
слагаемых. Доказывается формула бинома индукцией по  .
.
Разложим по формуле бинома выражения  и
и  .
.


Докажем неравенство  . Имеем:
. Имеем:
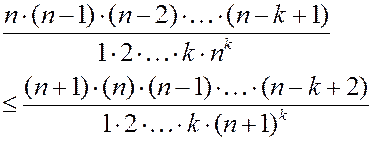 Û
Û

Теперь неравенство становится очевидным (каждый множитель слева не больше соответствующего по порядку множителю справа). Следовательно, уже первые  слагаемые в разложении
слагаемые в разложении  больше суммы всех
больше суммы всех  слагаемых в разложении
слагаемых в разложении  , то есть
, то есть
 .
.
Покажем, что последовательность  ограничена и не превосходит 3. Воспользуемся оценкой
ограничена и не превосходит 3. Воспользуемся оценкой

откуда

Сумма  оценивается сверху суммой геометрической прогрессии
оценивается сверху суммой геометрической прогрессии
 ,
,
откуда  для любого
для любого  . По теореме о пределе монотонной ограниченной функции существует предел
. По теореме о пределе монотонной ограниченной функции существует предел  при натуральных значениях переменной
при натуральных значениях переменной  . Этот предел был назван числом
. Этот предел был назван числом  и может быть вычислен с любой степенью точности.
и может быть вычислен с любой степенью точности.
Для доказательства существования предела при произвольных вещественных  можно воспользоваться очевидным неравенством
можно воспользоваться очевидным неравенством
 при
при  ,
,
и теоремой о двух милиционерах, с учетом того, что
 ,
,
 .
.
Можно показать, что предел  существует и равен
существует и равен  и при
и при  .
.
Пример. Вычислить предел 
Решение.




Лекция 9
Следствия 1)  ,
,
2)  .
.
Доказательство. 1) Полагая  в формуле
в формуле  , получим
, получим  . Вычисляя натуральный логарифм от правой и левой частей формулы, получим
. Вычисляя натуральный логарифм от правой и левой частей формулы, получим
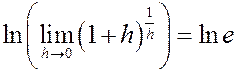 Û
Û 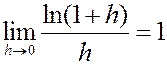 .
.
2). Полагая  Û
Û  , получим
, получим  .
.
Комбинирование пределов.
Пример. Вычислить предел
 .
.
Решение. Это неопределенность вида  . Действительно,
. Действительно,
 ,
,
откуда  .
.
Выполним тождественное преобразование

и воспользуемся формулой
 :
:


Следовательно,

Сделаем замену  .
.
Очевидно, что  при
при  . При этом
. При этом  , откуда
, откуда  . Получаем:
. Получаем:



Непрерывность и типы разрывов.
Если  или предела
или предела  вообще не существует, то говорят, что функция
вообще не существует, то говорят, что функция  имеет разрыв в точке
имеет разрыв в точке  . Всего имеется три типа разрывов.
. Всего имеется три типа разрывов.
1) Устранимый разрыв, когда существует  , но
, но  .
.
Пример. Доопределим функцию  при
при  значением
значением  . Поскольку
. Поскольку  , то функция
, то функция  окажется разрывной в точке
окажется разрывной в точке  . Однако, изменив значение функции
. Однако, изменив значение функции  всего в одной точке, мы получим в результате непрерывную функцию, то есть мы устраним разрыв.
всего в одной точке, мы получим в результате непрерывную функцию, то есть мы устраним разрыв.
2) Разрыв 1-го рода. Если существует предел слева  и предел справа
и предел справа  , но
, но  , то говорят, что функция
, то говорят, что функция  имеет разрыв первого рода с точке
имеет разрыв первого рода с точке  .
.
Пример. Рассмотрим функцию  и точку
и точку  . Имеем
. Имеем

При  предел отличается знаком:
предел отличается знаком:

Таким образом, точка  является точкой разрыва первого рода функции
является точкой разрыва первого рода функции  .
.
3) Все остальные разрывы считаются разрывами 2-го рода.
Пример 1.  ,
,  .
.
Если  , то
, то  . Если
. Если  , то
, то  .
.
Пример 2.  ,
,  . Если
. Если  и при этом
и при этом  ,
,  , то
, то  . Если
. Если  , но
, но  ,
,  , то тогда
, то тогда  . Таким образом никакого предела (ни справа, ни слева) у функции
. Таким образом никакого предела (ни справа, ни слева) у функции  в точке
в точке  нет.
нет.
Производные.
Определение. Число 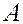 называется производной функции
называется производной функции  в точке
в точке  , если существует предел
, если существует предел

(предел отношения приращения функции  в точке
в точке  к приращению аргумента
к приращению аргумента  ).
).
Производная обозначается как  или как
или как  .
.







Для секущей графика  (прямой, соединяющий точки
(прямой, соединяющий точки  и
и  ) дробь
) дробь  равна угловому коэффициенту прямой
равна угловому коэффициенту прямой
 .
.
Здесь  обозначают координаты текущей точки секущей. Таким образом,
обозначают координаты текущей точки секущей. Таким образом,  показывает, насколько плавно (гладко) изменяется секущая при
показывает, насколько плавно (гладко) изменяется секущая при  .
.
Определение. Касательная к графику функции  в точке
в точке  есть предельное положение секущих при
есть предельное положение секущих при  .
.
Из определения следует, что уравнение касательной есть

Геометрический смысл производной состоит в том, что она является угловым коэффициентом касательной к графику функции  в точке
в точке  .
.
Физический смысл производной. Пусть  есть время, в течение которого материальная точка двигается вдоль прямой, а
есть время, в течение которого материальная точка двигается вдоль прямой, а  обозначает расстояние до некоторой точки отсчета
обозначает расстояние до некоторой точки отсчета  . Тогда функция
. Тогда функция  есть закон движения и определяет изменение положение точки со временем.
есть закон движения и определяет изменение положение точки со временем.
 |
0 
При такой интерпретации  есть расстояние, которое проходит материальная точка за время
есть расстояние, которое проходит материальная точка за время  . Следовательно, дробь
. Следовательно, дробь  есть средняя скорость движения за время
есть средняя скорость движения за время  . Переходя к пределу при
. Переходя к пределу при  , получаем, что
, получаем, что  есть мгновенная скорость движения, описываемого законом
есть мгновенная скорость движения, описываемого законом  . Это и есть физический смысл производной.
. Это и есть физический смысл производной.
Лекция 10.
Простейшие свойства производных.
Свойства пределов определяют следующие свойства производных.
1) 
2)  для произвольной константы
для произвольной константы  .
.
3) Если производная  в точке
в точке  существует, то функция
существует, то функция  непрерывна в этой точке.
непрерывна в этой точке.
Производные по определению.
Пример 1.  .
.


То есть 
Пример 2.  .
.


Таким образом, 
Пример 3.  .
.

Таким образом,
 .
.
Таблица производных от элементарных функций.

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Рассмотрим дифференцирование степенной функции при некоторых  .
.







Имеется два основных приема дифференцирования функций
1) Формуладифференцирования произведения и частного двух функций
 ,
,
 .
.
Доказательство. Докажем формулу дифференцирования произведения. По определению производной имеем:





2) Формула дифференцирования композиции (или сложной функции)
 .
.
Доказательство По определению производной имеем:



 .
.
Примеры.
1°) 

2°) 

3°) 
4°) 
5°) 
6°) 

Логарифмическая производная.
Рассмотрим функцию  .
.
Теорема.
 .
.
Доказательство. Прием, с помощью которого мы найдем производную функцию  , называется логарифмическим дифференцированием. Именно, прологарифмируем тождество
, называется логарифмическим дифференцированием. Именно, прологарифмируем тождество  , а затем найдем производную от правой и левой части.
, а затем найдем производную от правой и левой части.
 ,
,
 ,
,
 Ч.Т.Д.
Ч.Т.Д.
Пример.
1) 


откуда  .
.
2) 



Производной обратной функции.
Определение. Функция  называется обратной к функции
называется обратной к функции  если
если  ,
,  .
.
Примеры.
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  .
.
Теорема. Если  есть обратная функция к функции
есть обратная функция к функции  , то
, то
 .
.
Доказательство. Используя формулу для дифференцирования сложной функции, продифференцируем тождество
 .
.
Получаем:
 Û
Û  , Ч.Т.Д.
, Ч.Т.Д.
Пример. Найдем производную функции  . По теореме о производной обратной функции имеем:
. По теореме о производной обратной функции имеем:
 где
где  .
.
В силу основного тригонометрического тождества,
 .
.
Следовательно,
 .
.
Лекция 11.
Производная функции, заданной параметрически.
Пример. Циклоида.









Длина пройденного пути  равна, с одной стороны,
равна, с одной стороны,  , а с другой стороны,
, а с другой стороны,  (длина дуги). Следовательно,
(длина дуги). Следовательно,
 ,
,
 .
.
Обозначая  , получим
, получим

Функция, обратная к функции  , не может быть выражена через элементарные функции. Поэтому явное представление
, не может быть выражена через элементарные функции. Поэтому явное представление  также не может быть получено в классе элементарных функций.
также не может быть получено в классе элементарных функций.
Пусть  есть параметрическое представление функции
есть параметрическое представление функции  .
.
Теорема. 
Доказательство. Пусть  - функция, обратная к функции
- функция, обратная к функции  . Тогда
. Тогда  , поэтому
, поэтому

По теореме о производной обратной функции имеем  , где
, где  . Следовательно,
. Следовательно,
 . Ч.Т.Д.
. Ч.Т.Д.
Производная неявной функции.
Иногда функцию  можно задать неявно, посредством некоторого уравнения, зависящего от переменных
можно задать неявно, посредством некоторого уравнения, зависящего от переменных  и
и  :
:  .
.
В таком случае говорят, что функция  задана неявно.
задана неявно.
Пример 1.  Û
Û  .
.
Однако в явном виде выразить функцию  посредством элементарных функций можно не всегда.
посредством элементарных функций можно не всегда.
Пример 2.  .
.
Пусть точка  принадлежит множеству решений уравнения
принадлежит множеству решений уравнения  (то есть
(то есть  ), и пусть
), и пусть  - некоторая функция, удовлетворяющая условию
- некоторая функция, удовлетворяющая условию  . Как найти производную
. Как найти производную  ? Проще всего продифференцировать тождество
? Проще всего продифференцировать тождество  и, убедившись, что производная
и, убедившись, что производная  входит в получившееся выражение линейно, найти значение
входит в получившееся выражение линейно, найти значение  .
.
Продолжение примера 1.
 Û
Û  , откуда
, откуда
 .
.
В частности, если
 , то
, то  .
.
Проверка:  , При
, При  получаем
получаем  .
.
Основные теоремы
дифференциального исчисления.
Определение. Точка  называется точкой локального минимума функции
называется точкой локального минимума функции  , если для всех
, если для всех  из некоторого интервала
из некоторого интервала  выполнено соотношение
выполнено соотношение
 .
.
Если неравенство  заменить на неравенство
заменить на неравенство  , то точка
, то точка  будет называться точкой локального максимума функции
будет называться точкой локального максимума функции  .
.
Теорема Ферма. Пусть функция  определена на некотором интервале
определена на некотором интервале  и дифференцируема в точке
и дифференцируема в точке  . Тогда, если
. Тогда, если  является точкой локального минимума или максимума функции
является точкой локального минимума или максимума функции  , то
, то
 .
.
Доказательство. Пусть для определенности  является точкой локального минимума функции
является точкой локального минимума функции  . В определении производной функции
. В определении производной функции  в точке
в точке  рассмотрим предел справа:
рассмотрим предел справа:
 .
.
В числителе стоит положительная величина, так как по предположению  . В знаменателе выражение
. В знаменателе выражение  положительно, следовательно
положительно, следовательно  , и
, и  . Рассмотрим теперь предел слева.
. Рассмотрим теперь предел слева.

В числителе, по—прежнему, стоит положительная величина, а выражение  в знаменателе теперь отрицательно, следовательно
в знаменателе теперь отрицательно, следовательно  , и
, и  . Но тогда
. Но тогда  . Ч.Т.Д.
. Ч.Т.Д.
Теорема Вейерштрасса (без доказательства). Непрерывная функция, определенная на отрезке, достигает как своего минимум, так и своего максимума.
Теорема Ролля. Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в каждой точке интервала
и дифференцируема в каждой точке интервала  . Если
. Если  , то найдется точка
, то найдется точка  на интервале
на интервале  , в которой
, в которой  .
.







Доказательство. По теореме Вейерштрасса функция  достигает в некоторой точке
достигает в некоторой точке  отрезка
отрезка  своего максимума и в некоторой точке
своего максимума и в некоторой точке