Стохастическая сетевая модель. Граф передач и матрица вероятностей передач. Экспоненциальная стохастическая сетевая модель
Модель вычислительной системы может быть представлена как совокупность рассмотренных СМО, которые отображают отдельные устройства или группы однотипных устройств, а также связи между устройствами. Совокупность взаимосвязанных СМО называется стохастической сетевой моделью.
В конфигурации стохастической сети отражаются:
а) структура вычислительной системы;
б) последовательность выполняемых вычислительных этапов обработки информации.
Для простейших сетей в теории массового обслуживания принято:
а) входной поток l является простейшим;
б) длительность обслуживания n подчиняется экспоненциальному закону:
 ,
,
где U – поток равномерно распределенных случайных величин. Такие стохастические сети (модели) называются экспоненциальными. На основе конфигурации экспоненциальной стохастической модели формируются аналитические выражения, по которым непосредственно могут быть оценены характеристики системы.
В качестве примера рассмотрим следующую вычислительную систему (рис.1.8), в которую входят следующие подсистемы: S1 - процессор; S2 – быстродействующее ВУ (например, накопитель на магнитных дисках (НМД)); S3 – быстродействующее ВУ (например, накопитель на магнитных лентах (НМЛ)); S4 - группа однотипных медленно действующих ВУ(например, принтеры); S5 - канал передачи данных.

Рис. 1.8
В такой стохастической сети предполагается, что отсутствует последействие. Это означает, что все последующие события могут зависеть только от текущего события и не зависят от предшествующих событий. Такой процесс называется марковским. Он характеризуется множеством состояний S1 . . . S5 и матрицей вероятностей перехода в эти состояния. Вычислительный процесс всегда начинается с момента поступления заявки в процессор (состояние S1). Инициализация обращения к любому из устройств осуществляется только процессором. Связи между отдельными СМО устанавливаются в результате анализа порядка следования этапов обработки заявок. Для отображения вычислительного процесса используется направленный граф передач. Вершины графа соответствуют состояниям вычислительного процесса S1 , S2, … Sn, а дуги между вершинами указывают на связи между отдельными СМО (переход системы из одного состояния в другое). Дуги взвешиваются вероятностями перехода. Если система может перейти из одного состояния в одно из нескольких состояний, то возникает необходимость оценки вероятностей переходов. При этом строится матрица вероятностей передач.
Этап – процесс, завершающийся выходом заявки из процессора.
 Пусть имеем систему, модель которой в укрупненном представлении имеет вид, представленный на рис.1.9, где: S1 –процессор; S2, S3 – быстродействующие устройства; S4 – медленнодействующее устройство (например, принтер); S5 – селекторный канал; S0 – источник запросов.
Пусть имеем систему, модель которой в укрупненном представлении имеет вид, представленный на рис.1.9, где: S1 –процессор; S2, S3 – быстродействующие устройства; S4 – медленнодействующее устройство (например, принтер); S5 – селекторный канал; S0 – источник запросов.
Рис. 1.9
Граф вероятностей передач и матрица вероятностей передач представлены на рис. 1.10.
 |
Рис. 1.10
Здесь указаны вероятности перехода pji из j -ой подсистемы в i-ю. S0 - источник заявок (генератор заявок) в системе. Таким образам, число подсистем в системе (n+1), и размерность матрицы вероятностей передач соответственно тоже (n+1).
Рассмотрим, как оценивается вероятность перехода pji из j -ой подсистемы в i -ю. Для этого возьмём две вершины графа Sj и Si (рис.1.11) и тогда pji можно определить в виде
 ,
,
где 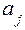 - весь суммарный (средний) поток, который исходит из подсистемы Sj;
- весь суммарный (средний) поток, который исходит из подсистемы Sj; 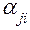 - средний поток заявок, который из подсистемы Sj поступает в Si; входной и выходной потоки равны.
- средний поток заявок, который из подсистемы Sj поступает в Si; входной и выходной потоки равны.
 i
i
Рис.1.11
Рассмотрим простейший пример расчета для системы на рис.1.9. Пусть S2 и S3 - внешние накопители. Имеется N файлов, которые распределены между накопителями S2 и S3. К каждому файлу при решении средней задачи должно быть осуществлено Dj обращений (j = 1, N). При каждом полном решении задачи на выходе системы появляется обслуженный запрос, который направляется к S0. Пусть также к внешнему устройству S4 при обслуживании средней задачи осуществляется d обращений.
Общее количество обращений к файлам D определяется в виде
D = 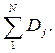
На выходе S1 заявка появляется (D + d + 1) раз.
Матрица вероятностей передач имеет вид, представленный на рис. 1.12.
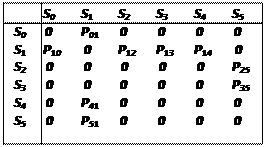 |
Рис.1.12.
Значения вероятностей передач определяются в следующем виде:
P01 = 1; P25 = 1; P35 = 1; P51 = 1; P41 = 1;
P10 =  ; P14 =
; P14 = 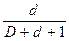 ; P12 =
; P12 =  ; P13 =
; P13 =  .
.
Суммы вероятностей передач по строкам должны удовлетворять соотношению
P10 + P12+P13+P14 =1.
§1.6. Разомкнутые и замкнутые стохастические сети. Параметры стохастических сетей
Для описания вычислительных систем используют следующие понятия:
а) разомкнутые стохастические сети (информационные системы оперативной обработки запросов, продажа железнодорожных билетов и т.п.);
б) замкнутые стохастические сети (работа вычислительной системы в многозадачном (пакетном) режиме). Эти системы не имеют чётко определённого входного потока запросов l; в данном случае источник запросов представляется как фиктивный в связи между выходом и входом.
 |
Рис. 1.16
Параметры стохастических сетей (исходные данные для расчёта исследуемой вычислительной системы):
1. Число СМО (S1, S2, . . . ,Sn ) - (n + 1).
2. Число каналов K1, K2, . . . ,Kn в подсистемах S1, S2, . . . ,Sn.
3. Матрица вероятностей передач P=[pji ]; 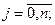
 .
.
4. l0 - средняя интенсивность источника заявок для разомкнутых сетей.
5. M - коэффициент многозадачности для замкнутых сетей.
6. n1, n2, . . . ,nn - длительности обслуживания, характеризующие задержки в подсистемах S1, S2, . . . ,Sn.