Релаксационные свойства аморфных полимеров в высокоэластическом состоянии

Согласно законам термодинамики всякий самопроизвольный процесс, происходящий в той или иной системе, приближает ее к состоянию равновесия. Однако если сам переход имеет конечную скорость, то в процессе перехода можно зафиксировать ряд промежуточных неравновесных состояний. Процессы, связанные с переходом системы из неравновесных состояний в равновесное, называются релаксационными.

Механические свойства любых реальных твердых тел, в том числе и полимерных, носят релаксационный характер. Ниже рассмотрены основные случаи проявления релаксационных свойств полимеров в высокоэластическом состоянии.

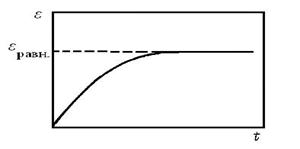
1. К образцу полимера приложено постоянное напряжение σ₀. Если при этом течение отсутствует, то напряжению σ₀ соответствует определенная равновесная высокоэластическая деформация ε_РАВН. Однако равновесная высокоэластическая деформация, соответствующая напряжению σ₀, достигается не мгновенно. Как видно из рис.18, равновесная деформация является верхним пределом, к которому во времени стремится реальная деформация.

Рис.18 Зависимость деформации полимера от времени при действии постоянного напряжения.

2. Образец полимера подвергают очень быстрой (практически мгновенной) деформации ε и закрепляют в деформированном состоянии. При этом в образце возникает напряжение σ₀, значительно превышающее равновесное напряжение σ_РАВН. Со временем в результате перегруппировки звеньев и изменения конформации макромолекул напряжение в образце уменьшается (рис.10). Этот процесс называется релаксацией напряжения.

Рис.19 Кривая релаксациинапряжения для каучука.

3. К образцу полимера приложено переменное напряжение, действующее, например, по синусоидальному закону σ=σ₀sinωt. В этом случае приложенное напряжение σ характеризуется двумя величинами — амплитудой σ₀и частотой ω (или периодом Т=2π/ω). Под действием периодических напряжений в образце возникают периодические деформации, также изменяющиеся по синусоидальному закону ε=ε₀sin(ωt–φ). Однако синусоида деформации сдвинута по фазе относительно синусоиды напряжения па угол φ, как это показано на рис.20. Возникновение разности фаз между напряжением и деформацией обусловлено релаксационными явлениями, вызывающими запаздывание изменений деформации по сравнению с соответствующими изменениями напряжения.

Рис.20 Сдвиг фаз между напряжением и деформацией при циклическом нагружении полимера.

В случае простых релаксирующих систем отклонение какой-либо измеряемой величины от равновесных значений уменьшается с течением времени по экспоненциальному закону:

(24)

где ∆x₀ и ∆х — отклонения значений измеряемой величины от равновесного значения для начального и данного моментов времени соответственно; τ —постоянная для данной системы, называемая временем релаксации.

Очевидно, что время релаксации характеризует скорость перехода системы в равновесное состояние. Зависимость деформации полимеров от времени при приложении к нему постоянной нагрузки (рис.18) можно описать уравнением ε=ε_РАВН(1—е^-^t^/τ), а процесс релаксации напряжения (рис.19) — уравнением σ–σ_РАВН=(σ₀–σ_РАВН)e^-^t^/τ.

В разных системах время достижения состояния равновесия различно. Например, скорости релаксационных процессов в жидкостях зависят, подобно вязкости жидкостей, от соотношения энергией межмолекулярного взаимодействия и теплового движения. Чем выше вязкость жидкости, тем медленнее протекают релаксационные процессы, т.е. тем больше времена релаксации. При комнатной температуре время релаксации обычных низкомолекулярных жидкостей мало и составляет 10^-8—10^-10 с. Однако при понижении температуры скорость молекулярных перегруппировок быстро уменьшается и при отсутствии кристаллизации жидкости при дальнейшем охлаждении превращаются в стеклообразные тела, обладающие бесконечно большим временем релаксации.

Очевидно, что время релаксации при прочих равных условиях должно зависеть от размеров молекул жидкости, возрастая при переходе от низших гомологов к высшим. Естественно было бы ожидать, что у полимеров, обладающих очень длинными молекулами, времена релаксации должны быть очень велики. Однако вследствие гибкости макромолекул релаксационные процессы в полимерах на самом деле характеризуются широким набором (спектром) времен релаксации, содержащим как очень малые времена, соответствующие перегруппировкам малых частей макромолекул, так и очень большие времена, соответствующие передвижению целых макромолекул или их больших участков.

Рис.21. Явление гистерезиса (стрелки на кривых указывают направление процесса деформации).

Релаксационные процессы обусловливают так называемый гистерезис, проявляющийся в несовпадении деформационных кривых ε=f(σ), получаемых при постепенном увеличении напряжения и при постепенном его уменьшении. При нагружении образца полимера деформация его за конечный промежуток времени не успевает развиться полностью. Следовательно, значения деформации оказываются меньше равновесных. При разгрузке образца он не успевает полностью сократиться и в каждый момент времени значение деформации оказывается больше его равновесного значения. Поэтому при неравновесной деформации кривые нагрузка — удлинение не совпадают. График, отражающий эти зависимости, имеет вид петли, которая называется петлей гистерезиса (рис.12). Площадь петли гистерезиса может быть представлена в виде суммы двух интегралов:

(25)

Площадь петли гистерезиса — это разность между удельной работой, затраченной при нагружении и полученной при разгрузке образца. Чем больше площадь петли гистерезиса, тем больше потери механической энергии. Эта энергия превращается в тепло и частично может затрачиваться на активацию сопутствующих химических процессов.

При переменном нагружении образца, когда напряжение изменяется по синусоидальному закону, необратимо затраченная за один цикл удельная работа деформации A=πσ₀ε₀sinφ тем больше, чем больше разность фаз напряжения и деформации.

Явление гестерезиса необходимо учитывать при создании изделий из полимерных материалов, работающих в режиме циклического нагружения. Очевидно, что при изготовлении, например, автомобильной шины механические потери следует максимально уменьшить, так как в противном случае при эксплуатации шины будет происходить разогрев материала, способствующий его разрушению.

Рассмотрим более детально релаксационные явления при деформации полимеров в широком интервале температур. Для этого проанализируем процесс развития деформации под действием синусоидально изменяющегося напряжения с постоянной амплитудой.

Рис.22 Зависимость амплитуды деформации полимера ε от температуры при различных частотах действия силы ω (ω ₁> ω₂> ω₃).

На рис.22 показана зависимость амплитуды деформации от температуры при различных частотах (или периодах) действия силы. Из рисунка следует, что при низких температурах (в области стеклообразного состояния) амплитуда деформации очень мала и практически не зависит от частоты действия силы. В облаети стеклообразного состояния время релаксации намного больше времени деформации, поэтому практически сколь угодно длительный промежуток времени оказывается недостаточным для перегруппировки звеньев макромолекул. С повышением температуры время релаксации уменьшается, так как вследствие увеличения интенсивности теплового движения звеньев их перегруппировки происходят чаще. При высоких температурах в области высокоэластического состояния время релаксации звеньев очень мало и в образце практически при любом значении времени действия силы высокоэластическая деформация успевает развиться до значений, близких к равновесному. Поэтому в этой области температур амплитуда деформации также практически не зависит от частоты действия силы.

Однако для каждого полимера существует такой интервал температур, в котором время релаксации и время развития деформации соизмеримы. В этой промежуточной области температур (переходная область из стеклообразного в высокоэластическое состояние) наблюдается резкая зависимость амплитуды деформации от частоты действия силы. Если время действия силы больше времени релаксации τ, деформация успевает развиться. Если время действия силы меньше времени релаксации τ, высокоэластическая деформация не успевает развиться. Так, если при некоторой температуре и частоте действия силы ω₃ в материале развивается деформация, близкая к равновесной, то при этой же температуре и частоте действия силы ω₁ (рис.22), амплитуда деформации может быть очень мала и материал ведет себя как стеклообразное тело.

Следует отметить, что наличие у полимеров спектра времен релаксации приводит к наложению сдвигов фаз, вызываемых различными релаксационными процессами. В результате этого наложения получается один пологий максимум сдвига фаз, охватывающий значительный интервал температур.

Как уже отмечалось, вследствие возникновения сдвига фаз между напряжением и деформацией (φ) в каждом цикле деформации необратимо затрачивается работа, которую можно рассчитать по формуле A=πσ₀ε₀sinωt. Поскольку практически вся работа, необратимо затраченная за цикл деформации, превращается в теплоту, то эффект теплообразования должен зависеть от частоты и температуры так же, как от них зависит произведение величин ε₀ и sinφ.

В стеклообразном состоянии величины ε₀ и sinφ близки к нулю, а следовательно, и потерн работы деформации за цикл также близки к нулю. В развитом высокоэластическом состоянии ε₀ достигает максимума, но значение sinφ близко к нулю (так как φ близко к нулю), а следовательно, и потери за цикл также незнательны. Таким образом, и частотная, и температурная зависимость механических потерь за цикл проходят через максимум, лежащий в области частот и температур промежуточных между частотами и температурами стеклообразного и развитого высокоэластического состояния.

Принцип температурно-временной суперпозиции. Сравнение кривых, представленных на рис.22, показывает, что увеличение частоты и понижение температуры одинаково влияют на деформацию или угол сдвига фаз. Одно и то же значение деформации или угла сдвига фаз можно получить, изменяя либо частоту, либо температуру. Это в определенном смысле свидетельствует об эквивалентности температуры и времени воздействия — так называемый принцип температурно-временной суперпозиции. Исходя из этого принципа, можно рассчитать зависимость механических свойств от частоты действия силы в столь широком диапазоне частот, который иногда вообще не может быть практически реализован в обычных лабораторных условиях. Это достигается проведением опыта в относительно узком диапазоне частот при разных температурах. Затем на основе принципа эквивалентности действия частоты и температуры строится единая обобщенная кривая при заданном значении температуры, охватывающая широкую область частот действия силы.

Рис.23 Обобщенная кривая релаксации напряжения полимера. Слева на рисунке кривые релаксации напряжения полимера при различных температурах (Т₆ > Т₅ > Т₄ > Т₂ > Т₁).

В качестве примера рассмотрим использование принципа температурно-временной суперпозиции для случая релаксации напряжения. На рис.23 приведены кривые релаксации напряжения полимера при различных температурах. Согласно принципу температурно-временной суперпозиции кривые релаксации напряжения, снятые при разных температурах, можно наложить на один обобщенный график путем простого их смещения вдоль оси логарифма времени на величину, зависящую от температуры. Выбрав в качестве температуры приведения Т₀ какую-либо произвольную температуру, например Т₅, станем сдвигать остальные кривые вдоль оси логарифма времени по отношению к стандартной кривой до тех пор, пока участки кривых не совместятся и не образуют одну обобщенную кривую, показанную на рис.15 (справа). Отрезок, па который следует сдвинуть каждую исходную кривую вдоль оси логарифма времени для получения обобщенной кривой, носит название фактора сдвига или параметра приведения а_Т. Фактор сдвига а_Т в первом приближении представляет собой отношение времени релаксации полимера при температуре Т к времени его релаксации при температуре приведения Т₀, т.е.

(26)

Таким образом, зависимость параметра приведения а_Т от температуры отражает температурную зависимость времени релаксации полимера. В методе приведения па самом деле очень важным оказывается правильный выбор температуры приведения или температуры отсчета Т₀. Если в качестве Т₀ выбрать, например, комнатную температуру, то характер зависимости параметра приведения от температуры для различных полимеров будет неодинаков. Он зависит от их химической природы. В то же время установлено, что все полимеры при температурах, равноудаленных от температуры стеклования, при одинаковом молекулярно-массовом распределении имеют одинаковые времена релаксации. Поэтому если для каждого полимера в качестве стандартной температуры выбрать температуру стеклования Т_С и построить а_Т как функции разности между температурой опыта и Т_С, то окажется, что в большинстве случаев эти функции имеют одинаковый вид:

(27)

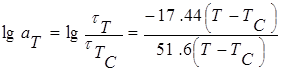
Принцип температурно-временной суперпозиции имеет большое практическое значение. Используя приведенные выше соотношения и методы обработки экспериментальных данных, можно получить информацию о механическом поведении полимеров при эксплуатации их в самых разнообразных условиях.