Лекция №2.

Сущность двойной записи

В результате хозяйственных операций происходит изменение средств предприятия и их источников. Каждая операция вызывает изменения не менее, чем в двух статьях баланса на одну и туже суму, т.е. приводит к двум экономическим явлениям, поэтому затрагивает две статьи. Материальная основа двойной записи – двойственность самого хозяйственного процесса. Расход материалов одновременно с его уменьшением на складе (кредит) означает увеличение производственных затрат, т.е. стоимости будущего продукта.

Двойная запись – это когда дебетуются один счет и кредитуется второй на одну и туже сумму.

Корреспонденция счетов– бухгалтерская запись между счетами. Счета участвующие во взаимосвязи – корреспондирующие. Запись указывающая дебит и кредит – бухгалтерская проводка (коунтировкой). Проводки могут быть простыми и сложными. Простая – когда сумма хозяйственной операции записывается в дебит одного и кредит другого счета. Сложная – дебетуется один счета и кредитуются несколько (два и более) и наоборот.

 

 

2.6. Пассивные связи и лишние степени свободы.

2.7. Замена высших пар 4 класса эквивалентными КЦ с низшими парами 5 класса.

2.8. Структурная классификация плоских механизмов по Ассуру-Артоболевскому.

3. Кинематический анализ плоских рычажных механизмов.

3.1. Цель кинематического анализа.

3.2. Методы решений.

3.3. Необходимые данные для выполнения кинематического исследования.

3.4. Понятие о масштабе.

3.5. Графоаналитический метод (метод планов скоростей и ускорений).

3.5.1. Проведение структурного анализа механизма.

3.5.2. Определение скоростей.

3.5.2.1. Определение скорости в н.м.

3.5.2.2. Определение скорости в группе Ассура.

3.5.2.3. Построение плана скоростей.

3.5.2.4. Определение скоростей заданных точек.

3.5.3. Определение ускорений.

3.5.3.1. Определение ускорений точек в н.м.

3.5.3.2. Определение ускорений точек в гр. Ассура

3.5.3.3. Построение плана ускорений.

3.5.3.4. Определение ускорений заданных точек.

 

2.6. Пассивные связи и лишние степени свободы.

В механизмах могут встречаться кроме степеней свободы звеньев и условий связей, активно воздействующих на характер движения механизмов, степени свободы и условия связи, не оказывающие никакого влияния на характер движения механизма в целом.

Лишние степени свободы, избыточные или пассивные связи – степени свободы и условия связи не оказывающие никакого влияния на характер движения механизма в целом.

Удаления из механизмов звеньев и КП, которым эти степени свободы и условия связи принадлежат удаление их не изменяет общего характера движения механизма в целом.

Например:

Звено 4 введено для увеличения жесткости конструкции. При структурном анализе звено 4 необходимо убрать

n=4

P5=6

W=2*4-2*6

W=12-12=0 ферма.

W=3*3-2*4=1

Можем вращать ролик 4 не оказывая влияния на механизм в целом.

 

Трение качения

Пружина применена для силового замыкания звеньев. Ролик служит для замены трения скольжения трением качения. Они характер движения звеньев не меняют.

W=3*3-2*3-1*1=2

W=3*2-2*2-1*1=1

 

 

2.7. Замена высших пар 4 класса эквивалентными КЦ с низшими парами 5 класса.

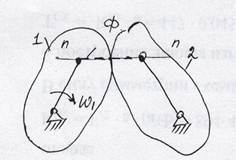
До замены: W= 3*2-2*2-1*1=1

После замены: W=3*3-2*4=1

 

 

Так как заменяющая цепь эквивалентна заменяемой, то:

1) W КЦ до замены и после замены не должны изменяться.

2) Не должен изменяться и характер относительного мгновенного движения звеньев.

3) Замена действительна только для данного положения механизма.

4) При замене всегда добавляется дополнительное звено Ф.

 

Алгоритм замены:

1) провести общую нормаль в точке касания профилей.

2) На нормали определить положения центров кривизны взаимодействующих поверхностей.

3) шарнирные концы фиктивного звена совместить с центрами кривизны.

4) Так как для прямолинейного профиля центр кривизны в ∞, то вместо шарнира в ∞ на прямолинейном профиле расположить ползун.

 

 

Примеры:

Элементы – кривая а и кривая b

n=2 n=3

P5=2 P5=4

P4=1 W=3*3-2*4=1

W=3*2-2*2-1*1=1

 

 

Элементы – точка - кривая

n=2 N=3

P5=2 P5=4

P4=1 W=3*3-2*4=1

W=3*2-2*2-1*1=1

 

 

Элементы прямая и кривая

 

 

Элементы точки прямая

Кинематические пары 4 класса обычно заменяются двумя КП 5 класса и одним звеном. При такой замене мгновенное движение звеньев не изменяется.

 

2.8. Структурная классификация плоских механизмов по Ассуру-Артоболевскому.

Русским ученым Л.В.Ассуром в 1914 году был впервые сформулирован основной принцип образования механизмов.

Асур догадался расчленить сложный механизм на структурные элементы с W=0 , что существенно упростило проведение анализа или синтеза.

Так как все высшие пары на плоскости могут быть заменены на низшие пары 5 класса, Асур рассматривал только КЦ с парами 5 класса (шарнирами и ползунами).

По Асуру любой сложный механизм может быть получен из НМ путем последовательного присоединения к нему так называемых структурных групп Асура с четным числом звеньев и W=0.

За структурную группу 1 класса Асур принял начальное звено со стойкой и назвал его начальным механизмом (нм).

 

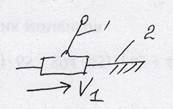
Электродвигатель Поршень

 

 

Количество НМ должно быть частично равно числу степеней свободы механизма W.

Условия присоединения: Группа элементами не присоединяется к одному и тому же звену.

Группы Асура - это такие КЦ, которые имеют:

1) нулевую степень свободы относительно тех звеньев, с которыми свободные элементы их звеньев входят в КП.

2) Не распадаются на более простые цепи, обладающие также нулевой степенью свободы.

Так как для групп Асура W=0, то

W= 3n – 2P5 =0

3n – 2P5 =0

3n = 2P5

n=2/3 *P5

Так как звено может быть только цельным

 

 

И т.д., то число звеньев в группе Асура всегда четное.

К структурным группам 2 класса Асур отнес группы, имеющие два звена и три КП 5 класса, то есть соответствующие первому соотношению

n/P5=2/3 – группы 2 класса второго порядка или двухповодковые группы.

Порядок группы определяется числом элементов звеньев, которыми группа присоединяется к основному механизму.

Структурные группы 2 класса имеют пять видов (см. таблицу)

Механизмы, в состав которых входят группы класса не выше второго, называются механизмами 2 класса.

К структурным группам 3 класса Асур отнес КЦ, в которых внутренние КП образуют треугольный замкнутый контур. (см. таблицу)

К структурным группам 4 класса Асур отнес КЦ, в которых внутренние КП образуют четырехугольный замкнутый контур. (см.таблицу)

2.9. Алгоритм структурного исследования

1.Определить степень подвижности механизма.

2.Удалить лишнее степени свободы и пассивные связи (проверить степень свободы).

3.Заменить высшие пары

(проверить степень свободы)

4.выделить группы Асура

5.Определить класс механизма:

- класс определяется по старшей группе, входящей в механизм.

-класс механизма определяется для проведения кинематического и силового анализа по классам.

 

Семейства механизмов по числу общих условий связи (пять семейств)

 

 

Группы Ассура

 

 

Прежде чем применить структурную формулу следует установить, сколько общих условий связи наложено на движение звеньев исследуемого механизма.

 

 

Примеры.

Кинематическая схема. Структурная схема.

 

 

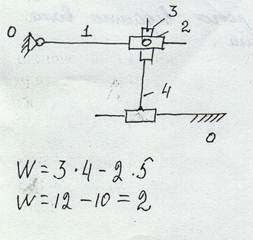
Кинематическая схема. Структурная схема.

 

3. Кинематический анализ плоских рычажных механизмов.

3.1. Цель кинематического анализа:

1)определение положений звеньев и траекторий движения отдельных точек.

2) определение скоростей отдельных точек и угловых скоростей звеньев.

3)определение ускорений отдельных точек и угловых ускорений звеньев.

3.2. Методы решений

1)аналитический

2)графоаналитический (метод планов)

3)графический (метод диаграмм)

3.3. Необходимые данные для выполнения кинематического исследования. При кинематических исследованиях должно быть известно:

1) схема механизма

2) размеры всех звеньев

3)закон движения воздушного звена.

3.4. Понятие о масштабе

Масштабный коэффициент К есть отношение истинной величины к отрезку, изображенному на чертеже.

Масштабный коэффициент К показывает количество истинных единиц изображаемой величины в одном мм чертежа.

 

Масштабы бывают:

-масштаб длины

 

-масштаб скорости

-масштаб ускорения

 

3.5. Графоаналитический метод (метод планов скоростей и ускорений)

Дано: OA, AB, BC, а

ω₁=const

ε₁=0

ω₄=const

ε₄=0

Определить: V _A,B,C ; W_A,B,C ; ω₂ ; ε₂

 

3.5.1 Проведение структурного анализа механизма

 

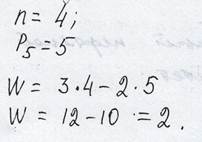
Следовательно, надо задать законы движения двух начальных звеньев.

НМ: 5-1 и 5-4 ; Группа Асура: 2-3 - 2 класс 2 вид ; Механизм 2 класса

 

1*.Формы задания законов движения начальных механизмов:

1)функция переменной

2)функция скорости

3)функция ускорения

 

1) Функция перемещений может быть задана в аналитической форме в виде соответствующей функции, связывающей перемещения начального звена со временем.

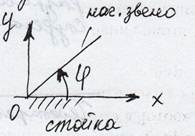φ=φ(t) , где

t – время

φ – угол поворота начального звена относительно неподвижной системы координат X0Y, связанной со стойкой.

 

Вращательная пара.

[Стр 71 ТММ]

Ускорение точки М в общем случаем вектор am состоит из:

1) нормального ускорения, направленного вдоль радиуса вектора rm;

2) тангенсального ускорения, направленного ┴ к радиусу вектора rm;

3) относительного релятивного ускорения, направленного вдоль радиус-вектора rm;

4) кориолисового ускорения, направленного ┴ к радиус-вектора rm.

Ускорение точки m звена k. Радиус вектор rm определяет положение точки.

Правило Жуковского Н.Е

Имеем т.M, к . движется с относительной скоростью Vr. Построим пл-ть П ┴ ωe угловой скорости переносного вращения и спроецируем Vr на эту пл-ть с обозначим Vr*

Модуль ускорения Кориолиса:

ak=2ωe Vr sin (ωe,Vr)

Vr*=Vr sin (ωe,Vr)

ak=2ωe Vr*.

Модуль ускорения равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, ┴ оси переносного вращения. Чтобы получить направление ak, следует вектор проекции относительной скорости Vr* повернуть на 90градусов вокруг оси, || оси переносного вращения в направление этого вращения.

В нашем примере Vr принадлежит плоскости ┴ оси переносного вращения.

ak ≡ 0 при 1) ωe=0, переносное движения являются поступательным при Vr=0, т.е в те моменты когда происходит изменения направления относительно движения 3) при sin (ωe,Vr)=0, когда ωe || Vr.

10* таким образом правило из ТМ

Если известия скорость какой-либо точки звена в переносном движении, то абсолютная скорость другой точки этого же звена определяется по теореме о сложении скоростей в переносном и относительном движениях.

Vабс=Vпер+Vотн

10.1* Векторное уравнение при вращательном относительном движении.

Va=Vo+Vao где

Va абсолютная скорость т.А

Vo переносная скорость т.А при поступательном движение

Vao относительная вращательная скорость т.А вокруг т.o вектор скорости т.А относительно т.o

Wa=Wo+W_ао^τ+W_aoⁿ

10.2*Векторное уравнение при поступательном относительном движении

Vb4- скорость в т.B4, принадлежащей в плоскости звена 4 и совпадающего в данный момент с т.B

-Vd вектор скорости т.D, он равен нулю

-Vb4d вектор скорости т.B4 относительно т.D

Vb4=Vb4d

 

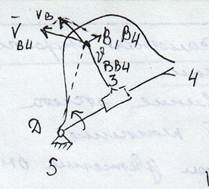Vb=Vb4+Vbb4

Wb=Wb4+Wbb4(r)+Wbb4(k)

Wbb4(r) - релятивное ускорение т.B относит т.B4

Wbb4(k) - ускорение Кориолиса т.B относительно т.B4

 

 

3.5.2 Определение скоростей

Определение скоростей начинаем с начальных механизмов HM, а затем, в каждой группе Асура, в порядке их присоединения

3.5.2.1 определением скорости точек в HM=5-1;5-4

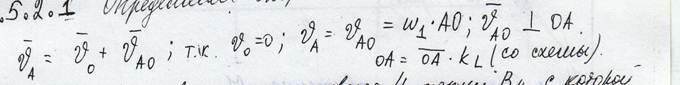Выделим в плоскости звена 4 точку B4, с которой в данный момент совпадает т.B

 

5.2.2 определяем скорости в группе Асура 2-3 II класс, 2 вид

 

Для определения направления V2 мысленно прикладываем Vba к т.B – против хода часовой стрелки TMM,с81

Для определения направления E2 мысленно прикладываем aτ к т.B – против хода часовой стрелки TMM с.85

3.5.2.3 Построение плана скоростей

Для построения плана скоростей задаемся масштабными коэффициентами

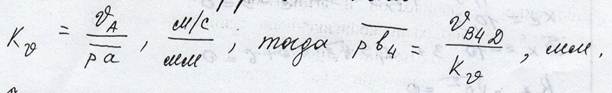Принимаем полюс p.

Пересечение лучей Vba и Vbb4 определяет в т.B

- определили из плана скоростей

 

 

3.5.2.4 Определение скоростей заданных точек

1. точка М принадлежит звену 2

Для определения скоростей т.М можно применить:

-метод подобия

-составить систему уравнений

Составим систему уравнений:

На плане скоростей проведем am┴MA

 

на плане скоростей проведем bm┴MB

 

 

2) Метод подобия

Справочник по математике, Бронштейн стр167

Треугольники, а также многоугольники подобны, если у них соответственные углы равны и сходственные стороны пропорциональны. Для подобия треугольников достаточно выполнения одного из следующих условий:

- три стороны данного треугольника пропорциональны трем сторонам другого

- два угла одного треугольника равны двум углам другого

-две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а заключенные между ними углы равны

 

Треугольник amb на плане скоростей и треугольника АМВ на кинематической схемы подобны по второму признаку подобия.

Правило: Если скорости двух точек звена известны, то сложно определить скорость любой третьей точки этого же звена по методу подобия. Для этого строят на плане треугольника амв ~треугольника АМВ на звене 2 с тем же направлением обхода ……… треугольников

Из подобия :

 

 

2. точка N принадлежит звену 2.

Составим векторное уравнения

но

следовательно направления вектора Vna и Vba совпадают

Скорости точек N и B относительно А пропорциональны расстояниям от этих точек до точки А.

Из плана скоростей:

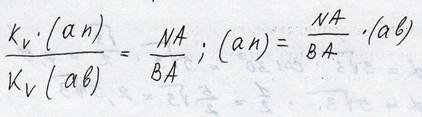
3. Точка К принадлежит звену 3

Выделим в плоскости звена 4 точку К4

 

3.5.3 Определение ускорений

3.5.3.1 определение ускорений точек в HM 5-1,5-4

3.6.3.2 Определение ускорений в гр.Ассура

3.5.3.3 Повторение плана ускорений

По плану ускорений определяем неизвестные ускорения

Задаемся масштабными коэффициентами

 

 

Определяем длины известных векторов и под нужными углами проведем их на плане. Полюс принят.

По полученному плану ускорений определяем неизвестные ускорения

Угловое ускорение звена 2

3.5.3.4 Определение ускорений заданных точек

1. точка Н принадлежит звену 2

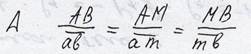Для определения ускорения точки М можно воспользоваться методом подобия, построив на плане треугольник амв ~треугольнику АМВ на звене 2 (с тем же направлением обхода вершин треугольников).

Из подобия

 

 

2.Точка К принадлежит звену 3

Составим уравнение

- величина известная, т.к. относительное движение поступательное

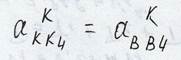- величина известная, т.к., т.к. движение поступательное

 

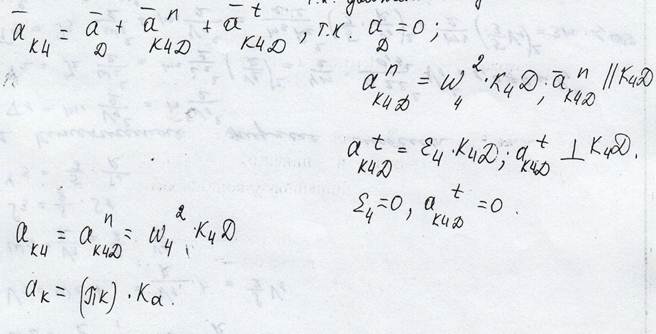
Для остальных видов групп Асура планы скоростей и ускорений строятся аналогично см. скоростей материал для построения планов скоростей и ускорений.