Пример 5.14.

Рис. 5.23. Рис. 5.24

 

 

Требуется, чтобы и в плоскости область устойчивости находилась слева от кривой D-разбиения, если двигаться от к . Левая сторона кривой штрихуется.

Рассмотрим в качестве примера кривую, изображенную на рисунке 5.24. На этой кривой показано, как надо наносить штриховку. Область устойчивости ограничена кривой со штриховкой внутрь.

Параметр по физическому смыслу есть величина действительная, поэтому для расчетов используется только отрезок действительной оси, охваченной кривыми со штриховкой внутрь:

от точки 1 до точки 2. (рис. 5.24) .

 

 

Пример 5.13

Дано характеристическое уравнение:

.

Пусть параметром будет , одно из значений которого =1 проставлено в уравнении. Надо найти, в каком интервале изменений характеристическое уравнение отвечает устойчивой системе автоматического регулирования.

 

Из уравнения:

 

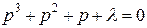
выделим: l(p) = - p³ - p² - p. Полагая p = jw , находим:

,

,

 

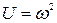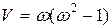
Полагая V(w) = 0, найдем частоты и точки пересечения кривой с осью абсцисс: w₁ = 0, U(0) = 0, w₂ = 1, U(1) = 1. Неограниченно увеличивая w выясним, что U ® ¥ и V ® ¥ , кривая уходит в бесконечность в верхней правой полуплоскости. В интервале 0 < w < 1 U < 1 и V < 0 . Для промежуточных значении U и V ход кривой уточняется заданием соответствующих частот. По совокупности данных строится кривая D-разбиения для положительных частот и дополняется зеркальным отображением. Наносится штриховка слева при движении по кривой от -¥ к +¥.

Результат показан на рис. 5.25. Интервал устойчивых значений l есть отрезок действительной оси от 0 до 1.

Контрольная проверка по критерию Гурвица для l = 0,5.

 

 

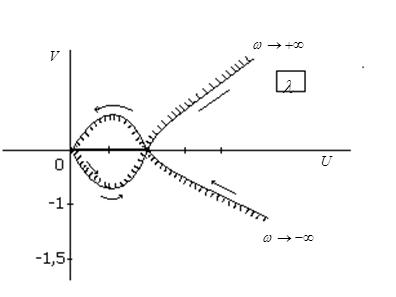
0,5 1

 

 

Рис. 5.25

 

Записываем характеристическое уравнение:

p³ + p² + p + 0,5 = 0 .

Коэффициенты: a₀ = 1, a₁ = 1, a₂ = 1, a₃ = 0,5. Действительно,

a₁a₂ - a₀a₃ > 0, система устойчива.

 

Дано характеристическое уравнение вида:

.

Требуется найти значения Т,при которых система будет устойчивой.

Назначив Т параметром, выделим :

Полагая 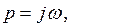получаем:

.

Запишем действительную и мнимую части:

 

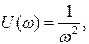
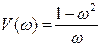
Анализ формул показывает:

- при w = 0 U = ¥, V = ¥;

- при w = 1 U = 1, V = 0; кривая V (U) пересекает действительную ось;

- при w = ¥ U = 0, V = -¥;

Кривая начинается в +¥ , пересекает ось абсцисс и неограниченно приближается к мнимой оси, уходя в -¥ .

Для уточнения хода кривой V (U) можно взять точки:

w = 0,5, U = 4, V = 1,5.

w = 2, U = 0,25, V = -1,5;

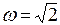, U = 0,5 V = -0,7;

w = 0,82, U = 1,5, V = -0,4.

Построив на плоскости U, V кривую для положительных частот, отображаем ее зеркально относительно действительной оси и получаем кривую для отрицательных частот, рис. 5.26. Нанеся штриховку, получаем область устойчивости. Устойчивость системы обеспечивают те значения параметра l , которые располагаются на отрезке действительной оси от 1 до ¥ . Контрольная проверка по критерию Гурвица подтверждает вывод.

 

V

1,5     0,5     -0,5   -1   -1,5

w → - ∞ w → 0

1.5

 

1

 

 

0.5

2 3 4 U

-0.5

 

-1

 

-1.5 w → 0

 

w → + ∞