Элементы финансовой математики
В теории и практике оценки недвижимости финансовая математика используется в основном для расчетов по доходному подходу. Главный принцип - принцип ожиданий, в соответствии с которым оценочная стоимость - это текущая (настоящая) стоимость (PV-present value) всех будущих выгод (доходов) от собственности, а также возможной ее продажи в конце периода функционирования. Это связано с тем, что оценщик оперирует денежными потоками в различные периоды времени (рис. 16).
| V | ||||||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| n | ||||||||||||||||||||||||
Цена приобретения
Оцененная стоимость (PV)
Рис. 16. Оперирование денежными потоками
В практике наблюдается огромное разнообразие значений ставок дохода, времени получения дохода, для этого расчеты с использованием сложных процентов и дисконтирования (приведение всех равномерных потоков денежных средств к одному моменту времени) были формализованы.
Аккумулирование –процесс приведения текущей стоимости денег к их будущей стоимости при условии, что эта сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование –процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
Понятия аккумулирования и дисконтирования базируются на определении сложного процента.
Сложный процент - это экономическая категория, используемая для сопоставления одной и той же суммы денег в различные периоды времени с учетом того, что в каждом периоде доход приносит не только первоначальная сумма вклада, но и процент от нее.
При начислении процентов 1 раз в год формула (1) выглядит следующим образом:
Sn = So • (1 + i)n,(1)
где Sn – сумма, накопленная через n-периодов;
So – первоначальная сумма;
i - ставка дохода;
n - количество периодов накопления.
При начислении процентов чаще, чем 1 раз в год формула (2) выглядит следующим образом:
Sn = So (1 + i/p)n•p,(2)
где Sn – сумма, накопленная через n-периодов;
So – первоначальная сумма;
i - ставка дохода;
n - количество периодов накопления.
p – количество периодов в году.
Ставка дохода на инвестиции –процентное соотношение между чистым доходом и вложенным капиталом.
В результате были установлены закономерности, получившие название 6 функций денежной единицы, представляющие собой специальные таблицы. Таблицы построены для определенного значения ставки процента. По вертикали расписаны возможные прогнозируемые сроки владения недвижимостью. По горизонтали – функции денежной единицы. В графах таблицы на пересечении строки и столбца расположены предварительно рассчитанные значения факторов сложных процентов.
В табл. 1 представлены шесть функций денежной единицы.
Таблица 1
Сводная таблица 6 функций
| F | Исходные данные | Требуется определить |
| F1 F2 F3 F4 F5 F6 | Текущая стоимость Серия равных платежей Будущая стоимость Будущая стоимость Серия равных платежей Текущая стоимость | Будущая стоимость Будущая стоимость Серия равных платежей Текущая стоимость Текущая стоимость Серия равных поступлений |
Перечислим эти шесть функций и их обозначения в экономических формулах. Обозначения в экономических формулах представлены в табл. 2.
Таблица 2
Основные обозначения
| Денежные понятия | Условия кредита | ||
| PV | текущая стоимость (present value) | N n | число лет число периодов |
| FV | будущая стоимость (future value) | I/y i | (номинальная годовая ставка процента (interest per year) ставка процента за период |
| PMT | платёж (payment), взнос, выплата | P/y | количество платежей в году (payments per year) |
Первая функция (F1) –накопленная сумма единицы.
F1 - аккумулированная сумма единицы – показывает какой по истечении времени будет стоимость единицы денежных средств, вложенных в доходную недвижимость:
FV = PV • (1 + i)n .(3)
Определение будущей стоимости при известной текущей показана на рис. 17.
| V | |||||||||

| FV | ||||||||
| PV | |||||||||
| n |
Рис. 17. (F1) –накопленная сумма единицы
return false">ссылка скрытаИногда при расчетах приходится сталкиваться с задачей определения количества периодов начисления, по истечении которых первоначально депонированная сумма увеличивается вдвое. Очень просто решить эту задачу позволяет правило 72 – х [3, с. 169].
Количество периодов, необходимых для удвоения первоначальной суммы вычисляются по формуле:
n =  . (4)
. (4)
Правило 72: удвоение вложенной суммы происходит через число лет, определяемое как частное от деления числа 72 на годовую номинальную ставку процента.
Правило 72 применимо в диапазоне от 3 до 18 % годовых.
Вторая функция (F2) – накопление единицы за период.
F2 – показывает, какой по истечении определенного срока будет стоимость серии периодических доходов в размере 1 денежной единицы, получаемых в конце каждого периода.
Если платежи происходят через строго определенные промежутки времени, то такая серия называется аннуитетом. Аннуитет -серия равномерных равновеликих платежей.
Аннуитеты разделяются на:
- равномерные –аннуитеты, состоящие из серии равновеликих платежей;
- неравномерные – аннуитеты, при которых величина платежей может быть разной в различных платежных периодах.
Базовая формула при платежах в конце периода и определение будущей стоимости обычного аннуитета представлены ниже.
FV = PMT •  . (5)
. (5)
FV
    
| |||||||||||||||||||||||
PMT
Рис. 18. (F2) – накопление единицы за период
Третья финансовая функция (F3) – фактор фонд возмещения капитала.
F3 –показывает, какими должны быть периодические доходы, получаемые в конце каждого периода в течение определенного срока владения объектом, с тем, чтобы к его окончанию была накоплена сумма в размере 1 денежной единицы.
Взнос на возмещение капитала - величина платежа, который необходимо депонировать (вкладывать) в каждом периоде при заданной ставке годового процента, чтобы в последнем периоде получить требуемую сумму капитала. Взнос на возмещение капитала подразделяется на:
- обычный- когда аннуитет возникает в конце периода;
- авансовый – когда первый платеж происходит одновременно с начальным поступлением, а последующие аннуитеты будут возникать через равные интервалы.
Если по условиям кредита необходимо вносить каждый месяц какой-либо оговоренный взнос, а в конце n-гогода погасить всю оставшуюся сумму, то величина этой суммы называется шаровой платеж.
Если величина взноса равна проценту в денежном выражении, то величина шарового платежа равна сумме кредита.
PMT = FV •  .(6)
.(6)
Определение платежа для накопления заданной суммы в будущем представлено на рис. 19.
FV
     
| |||||||||||||||||||||||
PMT
Рис. 19. (F3) – фактор фонд возмещения капитала
Четвертая финансовая функция (F4) - текущая стоимость реверсии.
F4– показывает текущую стоимость единицы денежных средств, получаемых в результате перепродажи недвижимости через определенный период времени.
Базовая формула при начислении процентов 1 раз в год:
PV = FV •  ,(7)
,(7)
Определение текущей стоимости при известной будущей стоимости представлено на рис. 20.
| V | |||||||||

| FV | ||||||||
| PV | |||||||||
| n |
Рис. 20. (F4) – текущая стоимость реверсии
Пятая финансовая функция (F5)- текущая стоимость аннуитета.
F5 – показывает текущую стоимость доходной недвижимости, приносящей периодический доход в виде серии платежей в конце каждого периода в размере 1 денежной единицы.
Базовая формула при платежах в конце года:
PV = PMT •  .(8)
.(8)
Текущая стоимость обычного аннуитета представлена на рис. 21.
    
| PV | ||||||||||||||||||||||||||||||||||||||||
PMT
Рис. 21. (F5)- текущая стоимость аннуитета
Шестая финансовая функция (F6) - взнос на амортизацию капитала.
Амортизация кредита –погашение долга по кредиту в течение определенного периода времени.
F6– показывает, какими должны быть периодические доходы в конце каждого периода в размере 1 денежной единицы текущей стоимости недвижимости в течение определенного срока владения объектом.
Базовая формула при платежах в конце года:
PMT = PV • 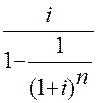 .(9)
.(9)
Определение платежей в счет погашения кредита на рис. 22.
| PV | ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||
PMT
Рис. 22. (F6) - взнос на амортизацию капитала