Правила вычисления предела
Чтобы вычислить  , необходимо.
, необходимо.
1. Попробовать подставить в функцию, стоящую под знаком предела,  . Если функция в этой точке непрерывна, в соответствии формулой
. Если функция в этой точке непрерывна, в соответствии формулой  предел равен числу
предел равен числу  .
.
2. Если точка 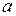 не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к
не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к 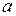 , то пределом является бесконечность.
, то пределом является бесконечность.
3. Если в результате подстановки получается неопределенность, то есть выражение вида  , следует раскрыть эту неопределенность, сделав сокращения, или привести получаемое выражение к замечательному пределу или его следствию.
, следует раскрыть эту неопределенность, сделав сокращения, или привести получаемое выражение к замечательному пределу или его следствию.
Примеры.
1.  .
.
2.  .
.
Неопределенности  показывает, что в числителе и знаменателе присутствуют бесконечно большие функции. Чтобы избавиться от них следует вынести самую большую величину в числителе и знаменателе за скобки, произвести сокращение, после чего еще раз применить пункт 1 правил.
показывает, что в числителе и знаменателе присутствуют бесконечно большие функции. Чтобы избавиться от них следует вынести самую большую величину в числителе и знаменателе за скобки, произвести сокращение, после чего еще раз применить пункт 1 правил.
Примеры.
1.  .
.
2.  .
.
Неопределенности  приводятся вначале к виду
приводятся вначале к виду  или
или  , затем раскрываются одним из перечисленных выше способов.
, затем раскрываются одним из перечисленных выше способов.