Задание 1. Построить график эмпирического временного ряда. Принять решение о возможности построения на его основе линейного тренда.
Л.В. Ишкова
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО ЭКОНОМЕТРИКЕ
Методические рекомендации студентам
по выполнению индивидуальных проектов
(на основе лабораторного практикума)
Новокузнецк 2013
Введение
В основу методических рекомендаций к выполнению индивидуальных проектов (в рамках лабораторного практикума по эконометрике) положено решение задачи на основе временного эмпирического ряда. Работа в конечном счете сводится к построению модели временного линейного тренда (или парной линейной регрессии) и сопровождается комментариями, практическими советами (например, при формулировании выводов после выполнения каждого задания).
Практикум состоит из 3-х этапов:
1-й этап. Для получения умений и навыков по выполнению эконометрического практикума студенты на начальном этапе работы выполняют первые 8 заданий практикума, решая сообща единую для подгруппы (или группы) задачу (она выдается преподавателем).
2-й этап. Каждый студент, накопив умения и навыки при решении общей задачи, получает у преподавателя задание для выполнения индивидуального проекта. Работа осуществляется в программе EXCEL. По окончании работы проект защищается и сдается отчет (на бумажном носителе).
3-й этап. Каждый студент выполняет индивидуальное задание по построению криволинейных парных регрессионных моделей (степенная, показательная и гиперболическая). При этом работа осуществляется только в электронном виде.
Примечание. Теория и практика лабораторного практикума по эконометрике более полно отражены в книгах: Л.В. Ишкова. Эконометрика для начинающих: теория и практика. Ч.1, Ч. 2., Новокузнецк, 2005 г. (есть в библиотеке НФ КемГУ в электронном варианте и на бумажных носителях).
Пример выполнения комплексного эконометрического проекта
(с комментариями)
Условие задачи. Эмпирический временной ряд представляет объем производства продукции предприятия (по месяцам) Yt за 10 месяцев 2002 года в сопоставимых ценах, млн.руб.:
| t | ||||||||||
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь |
| yt |
Задание 1. Построить график эмпирического временного ряда. Принять решение о возможности построения на его основе линейного тренда.
График эмпирического временного ряда строится в осях: t – время и yt – наблюдаемая величина (объясняемая переменная).
Для принятия решения с помощью построенного графика необходимо выявить присутствие или отсутствие в исходном ряду систематических смещений в характере разброса элементов (точек) ряда. Систематические смещения - это области на графике, где несколько (3 и более) последовательно лежащих точек оказываются по одну сторону от линии гипотетического (представленного мысленно) тренда.
Критерий принятия решения по 1-му заданию: Если исходный эмпирический ряд не содержит систематических смещений, то он является удобным для построения на его основе линейного тренда. При этом построенный тренд будет обладать хорошими прогнозными свойствами.
Задание 2. Вычислить математическое ожидание в ряду объясняемой переменной 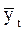 , ее исправленную дисперсию
, ее исправленную дисперсию 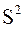 и исправленное среднее квадратическое отклонение
и исправленное среднее квадратическое отклонение 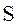 . На основе найденного исправленного среднего квадратического отклонения сделать вывод о возможности построения на основе эмпирического ряда линейного тренда.
. На основе найденного исправленного среднего квадратического отклонения сделать вывод о возможности построения на основе эмпирического ряда линейного тренда.
Среднее арифметическое значение (математическое ожидание) объясняемой переменной 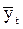 вычисляется по формуле:
вычисляется по формуле:
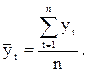
Исправленная дисперсия любой случайной величины (в том числе объясняемой переменной 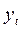 ) вычисляется по формуле:
) вычисляется по формуле:
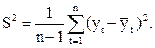
Для вычисления выше названных характеристик необходимо выполнить промежуточные вычисления. В программе EXCEL это необходимо сделать, организовав таблицу А (таблица A и все другие таблицы ориентированы на статистический ряд, предложенный для выполнения на его основе типового комплексного расчета):
Таблица A
Таблица промежуточных вычислений для отыскания дисперсии
наблюдаемой (объясняемой) переменной
| yt | 
| 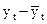
| ( 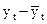 )2 )2
|
| ? | ? | ? | |
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
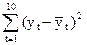 = ? = ?
|
На основе промежуточных вычислений находитсяисправленная дисперсия S(см. формулу выше).
Исправленное среднее квадратическое отклонение наблюдаемой переменной 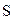 найдется по формуле:
найдется по формуле:
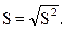
Далее необходимо сравнить порядок числового значения исправленного среднего квадратического отклонения с порядком чисел в ряду объясняемой переменной величины. Учесть, что порядком любого числа называется степень основания 10 –и в стандартном виде записи числа. Стандартный вид записи любого числа можно получить, выделив из него коэффициент, больший или равный 1 и меньший 10, т.е. стандартный вид любого числа В = 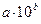 , где
, где 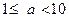 , b – порядок числа В.
, b – порядок числа В.
Пример: Пусть число В = 1231, 285. Запишем стандартный вид этого числа: В = 1, 231285 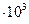 . Следовательно порядок этого числа равен 3.
. Следовательно порядок этого числа равен 3.
Критерий принятия решения по 2-му заданию.Если порядок числового значения исправленного среднего квадратического отклонения окажется меньше или равен порядку чисел в ряду объясняемой переменной величины, то исходный временной эмпирический ряд является однородным и на его основе может быть выявлена линейная тенденция (построен линейный тренд). При этом построенный тренд будет обладать хорошими прогнозными свойствами.
Задание 3. Осуществить линейное сглаживание эмпирического временного ряда методом скользящей средней (в данном практикуме по 5-и точкам ряда). Построить совмещенный график эмпирического и сглаженного рядов. Сделать вывод об их соответствии. Оценив визуально сглаженный ряд, сделать вывод о его монотонности. Принять решение о возможности построения на основе эмпирического ряда линейного тренда.
Для построения сглаженного ряда нужно скопировать исходный временной ряд, а в соседнем ряду вычислить точки сглаженного ряда ( 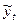 ).
).
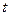
| 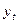
| 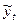
|
Если линейное сглаживание временного ряда осуществляется по m = 5 точкам, то сглаженные точки вычисляются методом скользящей средней по 5-и точкам, т. е. как средние арифметические значения соответствующих пяти последовательных значений эмпирического ряда. Таким образом, по выбранной методике найденная первая сглаженная точка является третьей в сглаженном ряду, найденная вторая – четвертой и т.д. Другим словами, все точки сглаженного ряда, начиная с третьей ( 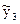 ) и заканчивая пред-предпоследней (
) и заканчивая пред-предпоследней ( 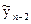 )находятся по базовой формуле:
)находятся по базовой формуле:
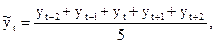
где yt – заданное значение элемента временного ряда;
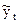 - сглаженное значение элемента временного ряда (t = 3, … , n – 2).
- сглаженное значение элемента временного ряда (t = 3, … , n – 2).
При этом теряются две первые и две последние точки ряда. Для их вычисления используют дополнительные эмпирические формулы:
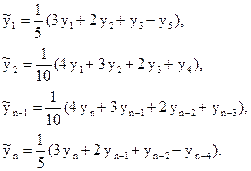
Далее строится совмещенный график исходного эмпирического и сглаженного рядов. В сглаженном ряду необходимо оценить наличие (или отсутствие) монотонности.Монотонность в ряду – это либо его постоянное возрастание или только его постоянное убывание.
Критерий принятия решения по 3-му заданию. Если в сглаженном ряду монотонность наблюдается, имеются все основания утверждать, что на основе эмпирического ряда может быть выявлена линейная тенденция (построен линейный тренд). При этом построенный тренд будет высокого качества, то есть он обладает хорошими прогнозными свойствами.
Задание 4. Провести автокорреляционный анализ эмпирического временного ряда (рассчитать последовательно коэффициенты автокорреляции между членами ряда 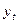 ; построить коррелограмму – график автокорреляционной функции; охарактеризовать структуру эмпирического ряда и выявить, между какими элементами эмпирического ряда наибольшая корреляция).
; построить коррелограмму – график автокорреляционной функции; охарактеризовать структуру эмпирического ряда и выявить, между какими элементами эмпирического ряда наибольшая корреляция).
Задачей автокорреляционного анализа временного ряда является установление степени и временного интервала зависимости последующих членов ряда от предыдущих. Наличие корреляционной связи между последующими и предыдущими членами ряда также служит информативным признаком временного ряда.
Коэффициенты автокорреляции рассчитывают по формуле:
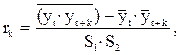
где 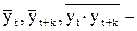 средние значения рядов yt, yt+k и
средние значения рядов yt, yt+k и 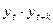 ; S1 и S2 – исправленные средние квадратические отклонения рядов yt и yt+k; k = 1, 2, … Следует учесть, что ряд
; S1 и S2 – исправленные средние квадратические отклонения рядов yt и yt+k; k = 1, 2, … Следует учесть, что ряд 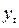 при отыскании коэффициентов автокорреляции непрерывно укорачивается на число элементов, равное значению
при отыскании коэффициентов автокорреляции непрерывно укорачивается на число элементов, равное значению 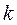 .
.
По определению, любой коэффициент автокорреляции должен попадать в интервал от –1 до 1, т.е. 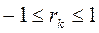 .
.
Средние значения величин 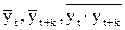 вычисляются по формулам:
вычисляются по формулам:
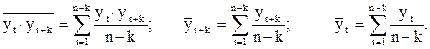
Исправленные средние квадратические отклонения вычисляются известным путем:
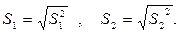
Значения коэффициента автокорреляции находятся для различных значений k: k = 1; k = 2; k = 3 и т.д. (в типовом задании до k = 5). В общем случае необходимо рассчитывать число коэффициентов автокорреляции, равное половине длины ряда + 1 (n/2 +1)
Алгоритм расчета первого коэффициента автокорреляции.
(k = 1)
Составляется таблица промежуточных вычислений для определения средних 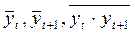 (таблица B, числовые данные в таблице соответствуют условию типового задания).
(таблица B, числовые данные в таблице соответствуют условию типового задания).
Таблица B
Таблица промежуточных вычислений для определения числителя коэффициента автокорреляции r1 при k = 1
| Средние | ||||||||||
| yt | ? | |||||||||
| yt+1 | ? | ? | ? | ? | ? | ? | ? | |||
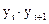
| ? | ? | ? | ? | ? | ? | ? | ? |
На основе таблицы A составляется таблица C промежуточных вычислений для определения исправленной дисперсии 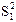 величины yt при k = 1:
величины yt при k = 1:
Таблица C
Таблица промежуточных вычислений для определения исправленной дисперсии величины yt при k = 1
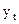
| 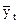
| 
| 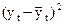
|
| ? | ? | ? | |
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
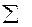 = ? = ?
|
Исправленная дисперсия в ряду yt при k = 1 будет находиться по формуле: 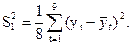 Исправленное среднее квадратическое отклонение в ряду yt при k = 1 будет равно:
Исправленное среднее квадратическое отклонение в ряду yt при k = 1 будет равно: 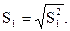
На основе таблицы A составляется таблица D промежуточных вычислений для определения исправленной дисперсии 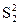 в ряду yt+1 :
в ряду yt+1 :
Таблица D
Таблица промежуточных вычислений для определения исправленной дисперсии величины yt+1 при k = 1
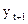
| 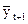
| 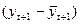
| 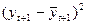
|
| ? | ? | ? | |
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
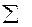 = ? = ?
|
Исправленная дисперсия в ряду yt+1 при k = 1 будет находиться по формуле: 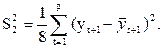 Исправленное среднее квадратическое отклонение в ряду yt+1 при k = 1 будет равно
Исправленное среднее квадратическое отклонение в ряду yt+1 при k = 1 будет равно 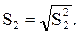
По результатам промежуточных вычислений для k = 1 определяется значение коэффициента автокорреляции r1.
Коэффициенты 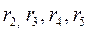 и т.д. находятся по аналогичному алгоритму.
и т.д. находятся по аналогичному алгоритму.
Последовательность полученных коэффициентов автокорреляции ряда данных называется автокорреляционной функцией временного ряда.
Коррелограммойназывают график (в виде столбчатой диаграммы) зависимости значений автокорреляционной функции (взятых по модулю) от времени наблюдения (порядка коэффициента автокорреляции). Строится коррелограмма в осях k – порядок коэффициента, r – значение автокорреляционной функции.
Анализ коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и условия, при которых связь между определенными элементами во временном ряду наиболее тесная (то есть при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру временного ряда).
Критерий принятия решений. Если в рассматриваемой задаче наиболее высоким оказался коэффициент автокорреляции первого порядка, то это означает, что исследуемый ряд содержит только тенденцию. Если же наиболее высоким оказался коэффициент автокорреляции порядка 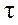 , то тогда ряд содержит не только тенденцию, но и циклические колебания с периодичностью в
, то тогда ряд содержит не только тенденцию, но и циклические колебания с периодичностью в 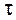 моментов времени.
моментов времени.
Задание 5. Определить степень 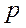 полиномиального тренда методом переменных разностей с использованием F-статистики (статистики Фишера).
полиномиального тренда методом переменных разностей с использованием F-статистики (статистики Фишера).
Этот метод заключается в вычислении переменных разностей и проверке гипотезы о равенстве дисперсий предыдущих и последующих разностей.
Сначала вычисляют первые разности:
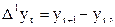
где t = 1, …, n – 1.
Затем по первым разностям вычисляют вторые разности:
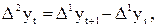
где t = 1, …, n – 2.
Далее последовательно вычисляются разности 3-го, 4-го и т.д. порядков (до m –го порядка):
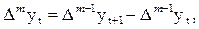
где t = 1, …, n – m.
На каждом шаге, начиная с m = 0, вычисляют:
a) дисперсии разностей m-го порядка по формуле:
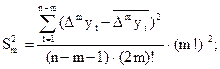
б) для каждых двух (предыдущей и последующей) дисперсий проверяют гипотезу о равенстве дисперсий по критерию Фишера:
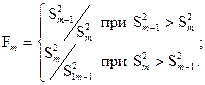
Проверка заключается в сравнении вычисленной статистики Фишера Fm c ее критическим значением Fкр = F (a, k1, k2), где a - принятый уровень значимости; k1 = n – m, k2 = n – m – 1(степени свободы).
Для 5% уровня значимости критические значения распределения Фишера приведены в таблице E.
Таблица E
| Степени свободы | Критические значения распределения Фишера | |||||
| ||||||
| 5,0 | 4,7 | 4,6 | 4,6 | 4,5 | 4,5 | |
| 3,3 | 3,0 | 2,8 | 2,8 | 2,7 | 2,7 | |
| 2,9 | 2,5 | 2,4 | 2,3 | 2,3 | 2,2 | |
| 2,7 | 2,3 | 2,2 | 2,1 | 2,1 | 2,0 | |
| 2,6 | 2,2 | 2,0 | 1,9 | 1,9 | 1,8 | |
| 2,5 | 2,2 | 2,0 | 1,9 | 1,9 | 1,8 |
Последовательность дисперсий 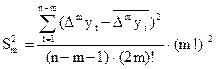 убывает с ростом m, и при некотором значении p = m – 1 выполняется неравенство Fm < Fкр (это означает, что сравниваемые дисперсии отличаются незначимо). В противном случае процедура вычислений разности и их дисперсий продолжается. Полученное значение p и является степенью полиномиального тренда.
убывает с ростом m, и при некотором значении p = m – 1 выполняется неравенство Fm < Fкр (это означает, что сравниваемые дисперсии отличаются незначимо). В противном случае процедура вычислений разности и их дисперсий продолжается. Полученное значение p и является степенью полиномиального тренда.
Поиск степени тренда начинается с составления таблицы переменных разностей G (данные приведены для типовой задачи).
Таблица G
Таблица переменных разностей
| t | 
| ||||||||||
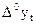
| ? | ||||||||||
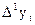
| -6 | -1 | -5 | ? | |||||||
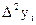
| ? | ? | ? | ? | ? | ? | ? | ? | ? | ||
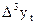
| ? | ? | ? | ? | ? | ? | ? | ? | |||
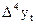
| ? | ? | ? | ? | ? | ? | ? | ||||
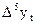
| ? | ? | ? | ? | ? | ? | |||||
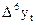
| ? | ? | ? | ? | ? | ||||||
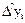
| ? | ? | ? | ? | |||||||
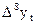
| ? | ? | ? | ||||||||
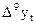
| ? | ? |
Далее необходимо приступить к вычислению дисперсий в рядах разностей.
Дисперсия разностей нулевого порядка (m = 0) совпадает с дисперсией эмпирического ряда (эта величина уже найдена во втором задании):
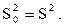
Дисперсия разностей первого порядка (m = 1) вычисляется по формуле:
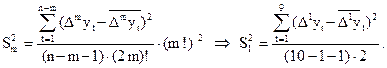
Составляется таблица промежуточных вычислений H.
Таблица H
Таблица промежуточных вычислений для отыскания дисперсии разностей первого порядка
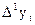
| 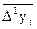
| ( 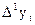 - - 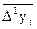 ) )
| ( 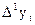 - - 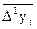 )2 )2
|
| ? | ? | ? | |
| ? | ? | ||
| ? | ? | ||
| ? | ? | ||
| -6 | ? | ? | |
| ? | ? | ||
| -1 | ? | ? | |
| ? | ? | ||
| -5 | ? | ? | |
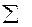 = ? = ?
|
После вычисления дисперсии разностей первого порядка проводится сравнение дисперсий разностей нулевого и первого порядков с помощью статистики Фишера. Выбирается формула для отыскания статистики Фишера (см. выше). Вычисляется статистика Фишера F1 и сравнивается с соответствующим критическим значением Fкр1 (в рассматриваемой типовой задаче для k1= n – m = 10 – 1 = 9; k2 = n – m – 1 = 8).
Критерий принятия решения. Если F1 < Fкр1 , то расчет дисперсий необходимо прекратить и по формуле p = m – 1 нужно рассчитать степень тренда (m – номер последней из рассчитанных дисперсий). В этом случае исследование в данном задании заканчивается.
Если же окажется, что F1 > Fкр1, сравнение дисперсий разностей необходимо продолжить. Для этого нужно вычислить очередную дисперсию  . Сравнив ее с
. Сравнив ее с  , найти статистику
, найти статистику  . Затем по таблице критических значений статистики Фишера определить соответствующее значение Fкр2 , Если окажется, что F2 < Fкр2 (т.е. критериальное условие выполняется), то найти степень полиномиального тренда и закончить исследование. Если же критериальное условие вновь не выполнится, исследование нужно продолжить.
. Затем по таблице критических значений статистики Фишера определить соответствующее значение Fкр2 , Если окажется, что F2 < Fкр2 (т.е. критериальное условие выполняется), то найти степень полиномиального тренда и закончить исследование. Если же критериальное условие вновь не выполнится, исследование нужно продолжить.
После того, как степень полиномиального тренда определена, необходимо записать общий вид соответствующего уравнения тренда.
6) Записать в общем виде уравнение линейного тренда (для р =1). Методом наименьших квадратов вычислить параметры линейного тренда по формулам:

Работая в программе EXCEL, для отыскания параметров тренда составить самостоятельно необходимую таблицу.